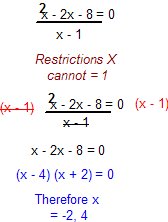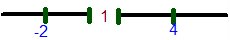Zeph's Notebook/Dictionary: Algebra

just to make things a bit organized, this scribe post is divided into two post. one section will be the circle geometry notes we took and the other post will be the algebra notes. this is so that this scribe post doesnt end up having the labels, circle geometry and algebra, at the same time.

Note: there is still more algebra notes to come from the next scribe!


REMINDERS:

~ FLICKR/NUMBER ASSIGNMENT - GET MORE PICTURES!! TOTAL OF 5 ALTOGETHER
~ "LOST IN MATHLAND" ASSIGNMENT DUE THE DAY AFTER TOMORROW!!
~ NO HOMEWORK
~ LAURESSA'S SCRIBE
~ GEOMETRY SET

Algebra Review

ALGEBRA REVIEW
LAST SCRIBE POST REVIEW BEFORE THE PRE-TEST!!!

in class, mr.k gave us equations to solve and two word problems.


SOLVING FOR X IN A GIVEN EQUATION


solve for x:

x + 3 = 4 - x

[(2x + 2)/(x^2 + 2x - 15)] + [2/(x - 3)] = 1/(x + 5)

√(w + 5) = √(3 - w) + 1


SOLVING FOR X IN AN ABSOLUTE EQUATION

x + 3 = 4 - x

since we are solving for x in an absolute value equation, x can only equal a positive number because the absolute value represents the distance and distance is always postive. because an absolute value of one side equals the absolute value on the other side, then there is more than one answer meaning that there are 4 equations.

we write down all the possible scenarios and since the absolute value operation means that whatever the number is inside the absolute value brackets, we're only look for its positive. for example, the absolute value of -3 is 3; OR -3 = 3.

mathematics is the science of patterns...

mr. k showed us that theres a pattern when solving for x in an absolute value equation. these are the possible solutions:

first, we remove one expression's absolute value brackets and there we are left with either a positive or a negative of that expression.

here are the possibilitites:

x + 3 = 4 - x;

x + 3 = -(4 - x);

-(x + 3) = 4 - x;

-(x + 3) = -(4 - x);

since we're looking for the positive value, all of these expressions have to be greater than 0.

wow...thats a lot of work just to solve for x but mr. k has lots of neat tricks up his sleeves so he showed us a shortcut.


"x + 3 = -(4 - x)" is the same things as "-(x + 3) = 4 - x" because all whats different is that a -1 was multipled on one side.

"x + 3 = 4 - x" is the same thing as "-(x + 3) = -(4 - x)" because all whats different is that a -1 was multipled on one side.

so really, we only need to solve for x for 2 equations which are:

x + 3 = 4 - x AND x + 3 = -(4 - x)


for x + 3 = 4 - x...

x + 3 = 4 - x
2x + 3 = 4
2x = 1
x = 0.5


for x + 3 = -(4 - x)...

x + 3 = -4 + x
x + 3 = x - 4

notice anything abnormal?

if we subtract both sides by x, then we get 3 = -4 which doesnt make sense.
if we add 4 to both sides we get 7 = 0 or if we subtrace 3 on both sides we get -7 = 0.

THIS IS AN EXTRANEOUS SOLUTION!

so for that equation, x = { }, N/A (not applicable), or "No Solution"

so x can only equal 1/2. BUT! we have to check if 1/2 fits perfectly into the given equation and it makes sense. so we sub in 1/2 for x.

x + 3 = 4 - x
(0.5) + 3 = 4 - (0.5)
3.5 = 3.5

both sides of the equation are equal so x = 3.5


in solving for x in an absolute equation, if the equation was like: x + 3 = 4 - x + 1, we have 4 different equations cuz a -1 isnt being multiplied on both sides. solve it and you'll see what i mean.

its like that because we are not looking for the absolute value of 4 - x + 1. we are solving for x when an absolute value equals another absolute value plus a number.

the next scribe after this lesson was sandy. oh and dont pick me for scribe the next day cuz i was already picked for scribe. its just that my name hasnt yet been crossed off cuz my scribe wasnt yet posted but now it is. so after today's scribe, i think cheriee's next cuz her name hasnt yet been crossed off so she's the next and last scribe. good luck and you'll do a great job like always!!

Algebra - Pre test day!

Hi guys! .. Well, sorry for the wait. By the way, HAPPY HALLOWEEN. (=

Today was a pretty easy class. We did a pretest, which wasn't included for marks. Everyone for the most part understood the first page. So I'll just briefly go over those questions first. =)

1. The sum and product of the roots of the quadratic equation 2x² + 2√(3)x - √(6) = 0 are:
A) √(3) and √(6)
B) -√(3) and √(6)/(2)
C) -2√(3) and -√(6)
D) -√(3) and -√(6)/(2)

The answer would be D. If we remember from previous class lessons, the sum is the negative of b, and the product is the same as c.


2. The Equation x² + 3x - 2 = 2 has:
A) 2 different negative numbers in its solution set.
B) only 2 solutions and they are both positive.
C) only two solutions
D) no solution
E) none of the above.

The answer for this question was A. This is how we solved it.
Case 1:
x² + 3x - 2 = 2
x² + 3x - 4 = 0
(x+4)(x-1) = 0
x = -4, x = 1
Case 2:
x² + 3x - 2 = -2
x² + 3x = 0
x(x+3) = 0
x = 0, x = -3

With these solutions, every single one will work when placed into the equation. Because two of the 4 solutions are negative (-), option A, is therefore true.

3. Solve: (2x)/(x-1) = (x)/(x+1) + 1

For this question, we're solving for x. So basically, you multiple each side by the LCD (Lowest Common Denominator). Which happens to be: 1(x-1)(x+1). By doing that we end up with this.
2x(x+1) = x(x-1) + (x+1)(x-1)

From here on, we solve for X.
2x² + 2x = x² - x + x² - 1
3x = -1
x = -1/3

Therefore the answer to this question is x = -1/3

4. Given the following quadratic equations, use the discriminant to determine which of the following have two real solutions.
A) 3x² + x - 2 = 0
B) x² - 2x + 1 = 0
C) -x² - 12x - 5 = 0

NOTE: The Discriminant is b² - 4ac

Now we solve each other them:

A) (1)(1) - 4(3)(-2)

1 + 24

25 <-- TWO REAL SOLUTIONS.

B) (-2)(-2) - 4(1)(1)

4 - 4
0 <-- ONE REAL SOLUTION.

C) (-12)(-12) - 4(-1)(-5)

144 - 20

124 <-- TWO REAL SOLUTIONS.

Therefore, A and B have two real solutions! .. =)

Time for the question we all seemed to be stumped on:

5. A river is 5 miles wide. A point C is 10 miles downriver from the point directly across the river from point A. Point B is x miles from the point directly across the river from A. A person swims 3 miles/hour from A to B and runs 5 miles/hour from B to C. Find x if it takes the person 3 hours and 20 minutes to travel from A to B to C.

Hint: Distance = (rate)(time)

First we start off with finding the total time it took for the person to get this distance.
Time: 3 h 20 min = 3 1/3 hrs or 10/3 hrs.

Secondly, we need to find AB, and BC.
AB:
- We know that by using the pythagorean theorem that a² + b² = c²
- Therefore x² + 5² = AB
- And √(x² + 25) = AB
BC:
- we know the total distance from the point directly across the river from A and C is 10 miles.
- Therefore BC = (10 - x)

Know that we know what AB and BC are, we can look for the equation.
swim time + run time = total time
√(x² + 25) / 3 + (10 - x) / 5 = 10 / 3

Now we find the LCD again and solve for x!
- First we multiply everything by 15, and we end up with this:
5√(x² + 25) + 30 - 3x = 50
5√(x² + 25) = 3x + 20
- To get rid of the radical we have to square both sides!
(5√(x² + 25))(5√(x² + 25)) = (3x + 20)(3x + 20)
25(x² + 25) = 9x² + 120x + 400
25x² + 625 = 9x² + 120x + 400
16x² - 120x + 225 = 0
- Now that we've found that and it isn't factorable, we use the quadratic formula to solve for x.
x = 120 ± √(14400 - 4(16)(225)) / 2(16)
x = 120 ± √(14400 - 14400) / 32
x = 120 ± √(0) / 32
x = 120 / 32
x = 60 / 16
x = 30 / 8
x = 15 / 4

And there you have it! .. This question covers most of the things we did in this unit. It's challenging, but it won't be on our tests nor our exam. So that's it! ..

Homework was posted by Mr. K earlier.
And our next scribe will be....
CRYSTA! . haha. have fun =)

why do we get extraneous solutions? (INTRO)

Hey everyone.
In the last few days we've been looking at radical equations, and when solving these equations (roots) we sometimes get extraneous roots. Well, this class was about: Why do we get these roots in rational equation.

LETS LOOK AT THESE Qs

This means: the graph can't touch 1 and has roots when x=-2 and 4
i.e.


Graphically this is what is going on

The green line is called the ASYMPTOTE. Its a line that goes as close as possible to the restricted value (in this case 1) but never touches it. Therefore you can have an output when x=0.999 or x=1.111 but not when x=1

HOW ABOUT IF WE WANT

In our case here, lets first see the sign changes in the intervals between -infinite to -2; -2 to 1; 1 to 4; and 4 to infinite, in order for us to determine when the equation < style="text-align: center;">
1st interval -ve infinite to -2
pick any number in the interval e.g -12
plug into the formula

2nd interval -2 to 1
pick any number in the interval e.g 0
plug it into the formula


3rd interval 1 to 4
pick any number in the interval e.g 2
plug it into the formula

4th interval 4 to infinite
e.g 1000 000
plug it into the formula
OBVIOUSLY the answer is positive

Applications with the Discriminant

Today in class Mr.K got us to do some questions on Applications with the Discriminant. Here are the questions and I'll go over them after:

1)For what values of k will the equation: 2x²+4x+(2-k-k²)=0 have exactly one root?
2)3x²-mx+3=0 a) For what value(s) of m will one root be double the other

b) For what value(s) of m will the roots not be real

1) Okay for question #1 we'll use the discriminant formula which is b²-4ac and in order to find k we need to know what the discriminant has to equal to ensure a 1 root parabola and the number is...0. So sub in a, b, and c into the Discriminant Formula

b²-4ac=0................................................Discriminant Formula
(4)²-4(2)(2-k-k²)=0......................And balance equation
16-8(2-k-k²)=0
16=8(2-k-k²)
2=2-k-k²
0=-k-k²
0=k+k²
0=2k
0=k

So after all that work we now know that k must equal to 0 in order to have the quadratic equation have only 1 root.

2)First we'll answer b) because it will be used to find a)

b)First we'll plug in the a,b, and c into the Discriminant Formula. We' ll set the equation to zero and solve for m. I'll show you:

m²-4(3)(3)=0
m²-36=0..............Notice that m²-36 is a difference of squares?
(m-6)(m+6)=0
m=6 m=-6

Now let's look at the values of m on the number line:
Explanation: If we pick a number less than -6 and more than 6 and sub it in for we'll get a positive result but we need a negative number in order to get no roots so the numbers we need are anything between -6 and 6. m=(-6,6)= No roots

a) Okay now for question a. What are the roots in the quadratic formula? They are:
x#1=-b-√(b²-4ac)..........x#2=-b+√(b²-4ac)
..............2a...............................2a

So the equation to find the roots for the questions in 2x#1(the lowest root)=x#2. Now with that in mind we sub in x#1 and x#2 with that equations above and sub in a,b, and c from the original equation and now we have.

2(m-√(m²-36)=m+√(m²-36)
...........6.............6

Now just solve for m and viola those are the roots.

Okay that's my third scribe and I hope this helps with some questions on Applications with the Discriminant. Homework for Mr.K's class is Exercise #18. The next Scribe will be...m@rk. Good night everybody.