Blogging on blobbing

HAppY HAlloWeeN Guys!! Whew! This unit went by so fast for me . I think that this unit is kinda easy for me except for the word questions. I wish we had more time practicing those word questions. All the other things in this unit is kinda just a review from grade 10 and my studies in the PHilippines. I hope that everything will turn out well tomorrow and everyone will get a good mark. Study well and good night. I still need to eat my candies.....

Bobby Bob Bob

This unit was alright. I didn't have much trouble because it's dealing with algebraic expressions, something i already know, but it also had to do with quadratic functions, something I'm not so good with. It's really annoying when you make a mistake, it's such a long process to correct it. Word problems are a problem and the quadratic formula mixes me up a lot. Well, that's about all I have to say about this unit and I hope that everyone studies and our marks are in the 80's! haha fingers crossed. Have a happy halloween and see you all tomorrow ^___^

-SAMUS

BOB

HAPPY HALLOWEEN GUYS ! okay well time for another test which means time for another bob. this unit wasn't that bad. some things take a long time to do like using the quadratic formula which means its more likely to make a mistake somewhere along the line. the toughest part in this unit would probably have to be the word problems but usually its because of overthinking. okay well i think i'm going to end my bob here. happy advanced christmas :)

BOB

Hello everyone!. Time for another test. This unit was a little harder then the previous units. I had a hard time following the long steps for the absolute value questions, we had like 4 cases for one questions. I always got confused on that. Everything else is okay, I just happen to mess up sometimes on the smallest thing to end up with the wrong answer. I think i need to slow down on them. That's all I have to say. GOOD LUCK!!!!

Algebra - Pre test day!

Hi guys! .. Well, sorry for the wait. By the way, HAPPY HALLOWEEN. (=

Today was a pretty easy class. We did a pretest, which wasn't included for marks. Everyone for the most part understood the first page. So I'll just briefly go over those questions first. =)

1. The sum and product of the roots of the quadratic equation 2x² + 2√(3)x - √(6) = 0 are:
A) √(3) and √(6)
B) -√(3) and √(6)/(2)
C) -2√(3) and -√(6)
D) -√(3) and -√(6)/(2)

The answer would be D. If we remember from previous class lessons, the sum is the negative of b, and the product is the same as c.


2. The Equation x² + 3x - 2 = 2 has:
A) 2 different negative numbers in its solution set.
B) only 2 solutions and they are both positive.
C) only two solutions
D) no solution
E) none of the above.

The answer for this question was A. This is how we solved it.
Case 1:
x² + 3x - 2 = 2
x² + 3x - 4 = 0
(x+4)(x-1) = 0
x = -4, x = 1
Case 2:
x² + 3x - 2 = -2
x² + 3x = 0
x(x+3) = 0
x = 0, x = -3

With these solutions, every single one will work when placed into the equation. Because two of the 4 solutions are negative (-), option A, is therefore true.

3. Solve: (2x)/(x-1) = (x)/(x+1) + 1

For this question, we're solving for x. So basically, you multiple each side by the LCD (Lowest Common Denominator). Which happens to be: 1(x-1)(x+1). By doing that we end up with this.
2x(x+1) = x(x-1) + (x+1)(x-1)

From here on, we solve for X.
2x² + 2x = x² - x + x² - 1
3x = -1
x = -1/3

Therefore the answer to this question is x = -1/3

4. Given the following quadratic equations, use the discriminant to determine which of the following have two real solutions.
A) 3x² + x - 2 = 0
B) x² - 2x + 1 = 0
C) -x² - 12x - 5 = 0

NOTE: The Discriminant is b² - 4ac

Now we solve each other them:

A) (1)(1) - 4(3)(-2)

1 + 24

25 <-- TWO REAL SOLUTIONS.

B) (-2)(-2) - 4(1)(1)

4 - 4
0 <-- ONE REAL SOLUTION.

C) (-12)(-12) - 4(-1)(-5)

144 - 20

124 <-- TWO REAL SOLUTIONS.

Therefore, A and B have two real solutions! .. =)

Time for the question we all seemed to be stumped on:

5. A river is 5 miles wide. A point C is 10 miles downriver from the point directly across the river from point A. Point B is x miles from the point directly across the river from A. A person swims 3 miles/hour from A to B and runs 5 miles/hour from B to C. Find x if it takes the person 3 hours and 20 minutes to travel from A to B to C.

Hint: Distance = (rate)(time)

First we start off with finding the total time it took for the person to get this distance.
Time: 3 h 20 min = 3 1/3 hrs or 10/3 hrs.

Secondly, we need to find AB, and BC.
AB:
- We know that by using the pythagorean theorem that a² + b² = c²
- Therefore x² + 5² = AB
- And √(x² + 25) = AB
BC:
- we know the total distance from the point directly across the river from A and C is 10 miles.
- Therefore BC = (10 - x)

Know that we know what AB and BC are, we can look for the equation.
swim time + run time = total time
√(x² + 25) / 3 + (10 - x) / 5 = 10 / 3

Now we find the LCD again and solve for x!
- First we multiply everything by 15, and we end up with this:
5√(x² + 25) + 30 - 3x = 50
5√(x² + 25) = 3x + 20
- To get rid of the radical we have to square both sides!
(5√(x² + 25))(5√(x² + 25)) = (3x + 20)(3x + 20)
25(x² + 25) = 9x² + 120x + 400
25x² + 625 = 9x² + 120x + 400
16x² - 120x + 225 = 0
- Now that we've found that and it isn't factorable, we use the quadratic formula to solve for x.
x = 120 ± √(14400 - 4(16)(225)) / 2(16)
x = 120 ± √(14400 - 14400) / 32
x = 120 ± √(0) / 32
x = 120 / 32
x = 60 / 16
x = 30 / 8
x = 15 / 4

And there you have it! .. This question covers most of the things we did in this unit. It's challenging, but it won't be on our tests nor our exam. So that's it! ..

Homework was posted by Mr. K earlier.
And our next scribe will be....
CRYSTA! . haha. have fun =)

Algebra Review Questions for Test Tomorrow

These two pages are a copy of an old test I used to give for this unit. Answers are not provided. Discuss your answers with your classmates in the comments to this post, together you'll figure it out, I know you will. ;-)

Remember ... learning is a conversation ... if you're not talking to somebody about it, you're not learning it ... let the conversation begin! ;-)

BOB 3

Hey guys! Today's Halloween! .. haha. I'll just assume that you guys are as excited as I am. (: Well, moving ahead. This unit went by pretty fast. I guess I pretty much know what I'm doing at this point, except for those absolute value questions that are supposed to have 4 cases? Those ones I'm having trouble understanding. But I think everything else is good to go and I don't have much else to say. haha SO...

Have a good Halloween guys! And good luck on your test on wednesday! (:

BOB TIMEE - Algebra/Radical Equations

Hey everyone!

Well time again for yet another BOB..
Well I think for me, and probably most of us, this past unit of Algebra/Radical Equations has flew by. It was a short and straight foward topic. I don't recall having a lot of troubles with this unit because of the simple grasp of solving for x. It actually has been one of my favoured and prefered units. Although, I expect it to get harder and more complex from here. The actual minor part that I may have troubles with is having to check the solutions and not understanding why its an Estraneous Solution. Well, actually it may have been that question our class had stumbled on today (which Mr.k had troubles understanding himself). Lets just hope theres none of those on the test.

Well good luck and good night! :)
also.. Happy advance Halloween!!

BOB for Algebra/Radical Equation Test

Hi it's me Ben :)
I see now that algebra is just an in-depth version of all the equations and formulas we've done before. But I'm wondering why some teacher say that we've been doing algebra since we first started math when my fellow classmates ask when we're starting algebra. I have some difficulty on the absolute value questions that have 2 absolute values on one side of an equation like: |x+1|-|2x-1|=5 (It's a random question I thought of. If it works out properly, cool).
I'm wondering how many cases will there be on a question like that?
That's my BOB for the Algebra Test. Good Night

why do we get extraneous solutions? (INTRO)

Hey everyone.
In the last few days we've been looking at radical equations, and when solving these equations (roots) we sometimes get extraneous roots. Well, this class was about: Why do we get these roots in rational equation.

LETS LOOK AT THESE Qs

This means: the graph can't touch 1 and has roots when x=-2 and 4
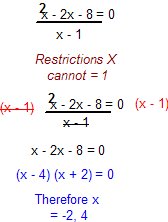
i.e.


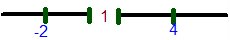
Graphically this is what is going on

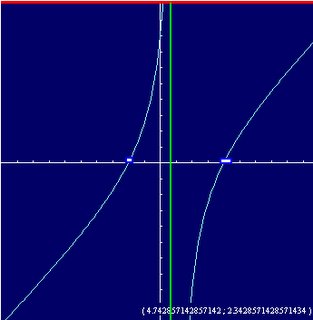The green line is called the ASYMPTOTE. Its a line that goes as close as possible to the restricted value (in this case 1) but never touches it. Therefore you can have an output when x=0.999 or x=1.111 but not when x=1

HOW ABOUT IF WE WANT

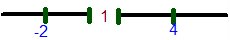In our case here, lets first see the sign changes in the intervals between -infinite to -2; -2 to 1; 1 to 4; and 4 to infinite, in order for us to determine when the equation < style="text-align: center;">
1st interval -ve infinite to -2
pick any number in the interval e.g -12
plug into the formula

2nd interval -2 to 1
pick any number in the interval e.g 0
plug it into the formula


3rd interval 1 to 4
pick any number in the interval e.g 2
plug it into the formula

4th interval 4 to infinite
e.g 1000 000
plug it into the formula
OBVIOUSLY the answer is positive

ABSOLUTELY ALGEBRA

Salutations,
in class today, for all you naughty kids that skipped (ha, no I'm just kidding), we worked on some problems that Mr. K had put up on the board. We mainly focused on algebraic equations that deal with extraneous solutions and we also had breifly discussed absolute. The four questions that the class worked on were:

x= √x-2 +4
x-4= √x-2
(x-4)(x-4)= (√x-2)(√x-2)
x²-8x+16= x-2
x²-9x+18= 0
(x-6)(x-3)
x=6 or x=3

*REMINDER: Always begin solving your algebraic equation by isolating the variable!

To check which answer is correct, we substitute the two solutions we got.
6= √6-2 +4
6= √4 +4
6= 2+4
6= 6
Therefore 6 is the correct answer.

3= √3-2 +4
3= √1 +4
3=5
The number 3 does not work out so we reject it. It is an extraneous solution.

√4x+5 - √2x-1= 2
√4x+5= 2+√2x-1
(√4x+5)(√4x+5)= (2+√2x-1)<2√2x-1)
4x+5= 4+4√2x-1 +2x-1
2x+2= 4(2x+1)
x+1= 2√2x-1
(x+1)(x+1)= 4(2x-1)
x²+2x+1= 8x-4
x²-6x+5=0

(x-5)(x-1)
x=5 or x=1

Check:
√4(5)+5 - √2(5)-1= 2
√25 - √9= 2
5 -3= 2
Therefore 2 work out and is the correct solution and 1 is the extraneous solution.

5r/ r²-9= 2
5r= 2x²-18
(multiply both sides by r-9 to get ride of it on the left)
0= 2x²-5x-18
(2x-9)(x+2)
x= 9/2 or x=-2

Check:
5(-2)/(-2)-9= 2
-10/-5= 2
2= 2
Therefore 2 is the correct answer and 9/2 is the extraneous solution.
x cannot equal 0, -4 because you cannot divide by 0!

1/x + 3/x+4= 2(x(x+4))
1(x+4)/x+4(x) + 3(x)/x+4 (x)= 2(x(x+4))
x+4 +3x= 2x²+8x
4x+4= 2x²+8x
0= 2x²-4x-4
0= x²+2x-2
x= -b ± √b² - 4ac/ 2(b)
x= -2 ± √4-4(1)(-2)/2(2)
x= -2 ± √12/2
x= -2 ± 2√3/2
x= -1 ± √3

*REMINDER: state restrictions before doing anything when dealing with fractions with vaiables in the numerator.

We'll go into more depth tomorrow about absolute numbers, but what we breifly discussed today is:
|5|= 5
|-5|= 5
|x|= 5
x= ±5

|x+1|= 2
case 1: x+1= -2
x= -3
case 2: x+1= 2
x= 1

Check:
|-3 +1| =2
|-2|= 2

|1 + 1|= 2
|2|= 2
Both solutions are possible.

|3|= -3
This is not applicable (N.A) because any absolute number must produce a solution that is positive.

|x-4|= 2x+1
case 1: x-4= 2x+1
x=2x+5
x=-5

case 2: x-4= -(2x+1)
x-4= -2x-1
3x=3
x= 1

Check:
|(-5)-4|= 2(-5)+1
|-9|= -9
5 does not work out, therefore it is an extraneous solution.

Check:
|1+4|= 2(1)+1
|3|= 3

Well that's about all we did in class. I hope this helps. Today we were not assigned any excercise, however, our homework for tonight is already posted up on the blog. Last, but not least, the next scribe......hmmmm who will it be next? I say, the SHEEP of the class is, THAT MEANS YOU NATNAEL!!!! muhahaha (evil laugh) take that sheep. I feel a hard class coming up tomorrow!

-SAMUS

Absolute Value Equations for Homework

Here it is folks .... your homework for tonight. You can use your graphing calculator to ceck your answers. If you don't know how to do that check oout the scribe post from today. If the scribe didn't post that, ask for it in the comments. ;-)

Rational Value Equations

Hey everyone,

Its me m@rk again. We start off today's short class with four questions.

The first question was:

√x+1 +2=4 REMEMBER: The first step is to isolate the radical by itself

√x+1=2 Square both sides to get rid of the radical sign

x+1=4 Subtract 1 on both sides

x=3 REMEMBER: Substitute your answer back at the equation and see if it makes sense.


The second question was:

x=√x+10 +2 Isolate the radical by itself

x-2=√x+10 Square both sides to get rid of the radical sign

(x-2) (x-2)= x+10 Distribute

x^2-4x+4 =x+10 Simplify it to an equation you are comfortable of doing

x^2-5x-6 = 0 Factor to find the roots

(x-6) (x+1) = 0

∴ x= 6,-1

Remember to substitute your answer in the original equation. In this question the
answer of -1 doesnt make sense, because it will not balance the equation. This case is called an extraneous solution.

The third question was:

4/x=3 , X ≠ 0 REMEMBER: WRITE THE RESTRICTIONS

4/x=3 Multiply both sides by the LCD to get rid of the fraction

4=3x

4/3=x Look at your resrictions if its not the same then it is not an extraneous solution


Lastly, the fourth question was:

4/x-3/x+1=1 , x ≠ 0,-1 REMEMBER: State your restrictions

4/x-3/x+1=1 Multiply both sides by the LCD

4x+4-3x =x^2+x Simplify

x^2-4=0 Factor

(x+2) (x-2)=0

∴ x=2,-2 Look back at your restrictions if its not the same, it is not an extraneous solution.

That's it for my scribe for today. Mr. K , we used the rest of the class time to do our homework. The lady was quite impress on how we focused till the last second of the class.

Our homework for tonight is Exercise #19. The next scribe is......... (background music:dun..dun...) the one and only SAMUS or should I say Mz. Anonymous. Good nyt and have fun.....

Applications with the Discriminant

Today in class Mr.K got us to do some questions on Applications with the Discriminant. Here are the questions and I'll go over them after:

1)For what values of k will the equation: 2x²+4x+(2-k-k²)=0 have exactly one root?
2)3x²-mx+3=0 a) For what value(s) of m will one root be double the other

b) For what value(s) of m will the roots not be real

1) Okay for question #1 we'll use the discriminant formula which is b²-4ac and in order to find k we need to know what the discriminant has to equal to ensure a 1 root parabola and the number is...0. So sub in a, b, and c into the Discriminant Formula

b²-4ac=0................................................Discriminant Formula
(4)²-4(2)(2-k-k²)=0......................And balance equation
16-8(2-k-k²)=0
16=8(2-k-k²)
2=2-k-k²
0=-k-k²
0=k+k²
0=2k
0=k

So after all that work we now know that k must equal to 0 in order to have the quadratic equation have only 1 root.

2)First we'll answer b) because it will be used to find a)

b)First we'll plug in the a,b, and c into the Discriminant Formula. We' ll set the equation to zero and solve for m. I'll show you:

m²-4(3)(3)=0
m²-36=0..............Notice that m²-36 is a difference of squares?
(m-6)(m+6)=0
m=6 m=-6

Now let's look at the values of m on the number line:
Explanation: If we pick a number less than -6 and more than 6 and sub it in for we'll get a positive result but we need a negative number in order to get no roots so the numbers we need are anything between -6 and 6. m=(-6,6)= No roots

a) Okay now for question a. What are the roots in the quadratic formula? They are:
x#1=-b-√(b²-4ac)..........x#2=-b+√(b²-4ac)
..............2a...............................2a

So the equation to find the roots for the questions in 2x#1(the lowest root)=x#2. Now with that in mind we sub in x#1 and x#2 with that equations above and sub in a,b, and c from the original equation and now we have.

2(m-√(m²-36)=m+√(m²-36)
...........6.............6

Now just solve for m and viola those are the roots.

Okay that's my third scribe and I hope this helps with some questions on Applications with the Discriminant. Homework for Mr.K's class is Exercise #18. The next Scribe will be...m@rk. Good night everybody.

Discriminant and the Nature of Roots.

Hello again. MERIAN here to fill you in on what we did today in class.

We first started with Mr. K giving us three equations.

f(x) = x² + 5x + 6
y= x² -4x - 5
f(x) = x² + 2x - 15

We were to find:

- The ROOTS
- The sum of the roots
- The ROOT PRODUCT

Here were the answers.

f(x) = x² + 5x + 6

ROOTS: x = -3, x = -2
ROOT SUM: (-2) + (-3) = -5
ROOT PRODUCT: (-2)(-3) = 6

y= x² -4x - 5

ROOTS: x = 5, x = -1
ROOT SUM: 5 + (-1) = 4
ROOT PRODUCT: 5(-1) = -5

f(x) = x² + 2x - 15

ROOTS: x = -5, x = 3
ROOT SUM: (-5) + 3 = -2
ROOT PRODUCT: (-5) 3 = -15

Afterwards, we were to compare our answers to the equation. Remember, mathematics is the science of Pattern--so look for a pattern.

We found out that the pattern here was that the root sum is the negative of B. Let's look at the first one as an example.

f(x) = x² + 5x + 6

ROOT SUM: (-2) + (-3) = -5

AND the other pattern was that The ROOT PRODUCT is = to C.

f(x) = x² + 5x + 6

ROOT PRODUCT: (-2)(-3) = 6

Knowing that there's a relation between them, we can easily figure out the roots of an equation just by simply looking at it. There's a catch though..

Mr. K then gave us another equation and asked us to find the roots of it, the sum of the roots and the product of the roots.

f(x) = x² + 6x + 10

This equation can't be factored out perfectly. it doesn't have REAL roots so it must have an imaginary root. But, since it's not factorable, the other thing we can do is use the Quadratic Formula.

REMINDER: i² = -1 OR i = √-1



x₁ = -3x + i
x2 = -3x - i

^those are your roots. To find out the product of the roots you must distribute -3x - i & -3x + i.
Like so.

( -3x + i )( -3 - i )
9 + 3i - 3i - i²
9 - i²
9 - (-1) = 10 <- The product of roots.

It's different when there is a number in front of a.

Example:

y(x) = 2x² + 5x - 3 <- You can't just take the root sum or root product just by looking at the equation at this point. Since there's a number in front of a it'll factor the other numbers resulting in a different number..

So to do this correctly you must find the coefficients and rewrite 5x. In this case it's going to be 2 & 3.



ROOT SUM
-1 + (-3)/2

-2/2 + (-3)/2

= -5/2

ROOT PRODUCT
(-1)(-3/2)
3/2

We should be also aware of number relationships. Here's a diagram for refrence.


In a quadratic formula, if the inside of a radical is negative then there are no roots. it discriminates the qualities of the equation.

DISCRIMINANTS:
b² - 4ac > 0 = ROOTS
b² - 4ac = 0 = 1 ROOT
b² - 4ac < 0 =" NO">

HOMEWORK IS EXERCISE 16
NEXT SCRIBE WILL BE.................benofschool

MERIAN's scribe!

Hey everyone~ I'm lucky to be scribe today. =)

Mr. K was away today so we had a sub. We only worked on Exercise 17 for the whole class.
I don't know what else to put down because that's all we did. No major problems or anything with the work, I believe.

Mr. K, if your reading, just to let you know, our class was very well behaved and we did our work nice and quietly. Too quiet actually.

I guess that's all for my scribe..I don't feel this is fair, so I'll just scribe again on Monday.

Have a good weekend guys.

Quadratic Formula

Hi guys! .. I'm Sandy and I'm your scribe.

Today we continued from yesterdays lesson and we started with this question.

1. a² - 3a - 15 = 0
To solve this, we had to use the quadratic formula.
a = 3 ± √(9 + -4(1)(-15))
                    2(1)
a = 3 ± √(69)
            2
Now lets change the numbers a bit.2. a² - 2a - 15 = 0
(a - 5)(a = 3) = 0
a = 5, a = -3
^^ Here, instead of using the quadratic formula (which would've worked as well) we simply factored it. Like Mr. K says, why use the sledge hammer when we can use the hammer?

Lets stop for a moment and see if we recognize any patterns in the following equation.
3. (x - 2/x)² - 2(x - 2/x) - 15 = 0
This is something we call a quadratic in form.
If we're to do something like this:
Let a = x - 2/x
we end up with an equation that looks like this:
a² - 2a - 15 = 0
Which happens to be the exact same equation as the one we did above. So have you seen the pattern??

Above, we figured out that the roots of the equation a² - 2a - 15 = 0 were a = 5 and a = -3.
AND
We Let a = x - 2/x as well.
So lets plug in what we need to and solve for question 3.

a = 5
x - 2/x = 5
Now multiply both sides by x to get rid of the x in 2/x.
x² - 2 = 5x
x² - 5x - 2 = 0
^^ Since that doesn't factor nicely, this is where we can use the quadratic formula.
x = -b ± √(b² - 4ac
                2a
x = 5 ± √(25 - 4(1)(-2))
                   2
x = 5 ± √(23)
            2
x₁ = 5 + √(23)
             2
x₂ = 5 - √(23)
             2

a = -3
For this one, we do it exactly the same way.
If you guys want to try it out and want to see if you did it right, here's the answer.
x = 3 ± √(17)
             2

**SOMETHING TO GET INTO THE HABIT OF DOINGLets look at another quadtraic in form:
4. x⁴ - 13² + 36 = 0
- Let a = x²
- a² - 13a + 36 = 0
- (a - 9)(a = 4)
- a = 9, a = -4
It should be pretty straight forward on how to get there, but if you have any questions, feel free to ask! =)
Anyway, this is where most people do this:
x² = 9, x² = 4
x = 3, -3, x = 2, -2
9 OUT OF 10 TIMES when you solve it this way, you'll forget the negative (-) solution
SOOOO..
Lets get into the habit of solving our equation this way:
x² - 9 = 0, x² - 4 = 0
(x + 3)(x - 3) = 0, (x + 2)(x - 2) = 0
x = -3 and 3 , x = -2 and 2
This way, there's no way you'll forget the negative (-) solution.

Okay. I hope this helped Sam! =) Get well soon! .. If you have any questions don't be shy to ask. :D

NEXT SCRIBE IS .. How'd you guess? MERIAN.

Homework tonight is Exercise 15. Have fun =)

Pop Goes The Quadratic Formula!

Today we derived (watch this!) the Quadratic Formula in all its glory!



Here it is explained.

You can practice using it over there!

Now sing it with me folks!



x equals negative b
plus or minus the square root
of b squared minus 4ac
all over 2a

Discovering THE QUADRATIC FORMULA

We started today's class with this simple question. .

FIND THE ROOTS USING 'COMPLETING THE SQUARE':
i) y=x²-6x-3
y=x²-6x+9-9-3
y=(x-3)²-12
* * Okay so first of all, we simply transfored our original equation from general form to standard form.

- NOW WE MUST ALLOW Y = 0
0=(x-3)²-12
12=(x-3)²
+-(12)^1/2=x-3
3+-2(3)^1/2=x

ii) y=2x²-8x+1
y=2[x²-4x+4-4]-1
y=2[(x-2)²-4]+1
y=2(x-2)²-7

0=2(x-2)²-7
7=2(x-2)²
7/2=(x-2)²
[7/2]^1/2=x-2
2[7/2]^1/2=x

Is there an EASIER APPROACH to find roots of all parabolas of the general form?
- YES. Yes there is!

Quick Note: y=ax²+bx+c
- represents ALL, yes every single parabola out there


CONVERTING THE GENERAL FORM TO THE STANDARD FORM FOR THE EQUATION OF A PARABOLA:

i) The General Form
y=ax²+bx+c

ii) Factor "a" out of all x-terms
y=a[x²+b/ax ]+c

iii) Find half the coefficient of the x-term & square it
1/2(b/a)=b/2a (b/2a)² = b²/4a²

iv) Complete the square
y=a[x²+b/ax+(b/2a)²-(b/2a)²]+c

v) Factor and Simplify
y=a[(x+b/2a)²-b/4a²]+c

vi) Distribute "a". Find common denominator
y=a(x+b/2a)²-b²/4a+(4a/4a)c

vii) Add Fractions
y=a(x+b/2a)²+-b²+4ac/4a

IN CONCLUSION..
Reference: y=a(x-h)²+k

h= -b/2a
**REMEMBER THAT!

k= -b²+4ac/4a
**YEAH, THATS UGLY


FINDING THE ROOTS OF A PARABOLA FROM THE EQUATION IN GENERAL FORM CONTINUED FROM ABOVE:

i) Set to "zero"
0=a(x+b/2a)² + -b²+4ac/4a

ii) Add b²+4ac/4a to both sides
b²+4ac/4a=a(x+b/2a)²

iii) Mulitiply both sides by 1/a

b²-4ac/4a²=(x+b/2a)²

iv) Find the square root of both sides
[b²-4ac/4a²]^1/2 = x+b/2a

v) Simplify Radical
-b/2a+-[b²-4ac/2a]^1/2=x+b/2a

vi) Add -b/2a to both sides
-b/2a+-[b²-4ac/2a]^1/2=x

IN CONCLUSION...
vii) We add the fractions and get
(dun dun dun..) THE QUADRATIC FORMULA!

x= -b+-[b²-4ac]^(1/2) / 2a

REMEMINDER: It is important to remember this specific formula!

So for the finale of my scribe- heres our handy sing along.
(8).. X equals negative b,
plus or minus the square root of b square,
minus 4ac, all over 2a
.

.

.
REMINDER: In order to transfer information from short term memory into long term memory, take in the information SIX TIMES.

Okay, my times up guys. Hope you enjoyed
- Homework assignment: Exercise #14

sandy you're next!

- - Nightt :)

Trigonometry; definitions

In class we put new things in our math dictionaries. If you don't have them, then grab a pen or pencil and a piece of paper and jot these down.
* Represents a beginning to a new page.
Examples are in purple.

Using the Factored Form:

1. You can quickly find the roots by solving the quadratic.
example: 0= x² + 5x + 6
0= (x+2)(x+3)
x= -2 x= -3
Roots at x= -2, x= -3

2. You can find the x-coordinate of the vertex by finding the midpoint of the roots.
example: Xv= (-2) + (-3) / 2
Xv= -5/2

3. Once you know the x-coordinate of the vertex you can substitute back into the equation to find the y-coordinate of the vertex.
example: F(-5/2) = (-5/2)² + 5(-5/2) + 6
F(-5/2) = -1/4
Therefore the vertex is at (-5/21, -1/4)

The General Form for the Equation of a Parabola:
F(x) = ax² + bx + c

The Role of Parameter b:
b produces an obligue translation.

The Role of Parameter c:
c is the y-intercept of the parabola. It's coordinates are (0,0)

*Completing the Square:

PROCEDURE:
1. Factor the coefficents of x² out of the two
terms. Leave some "space" in the brackets.
y= 3x² + 12x -5
y= 3(x² + 4x )-5

2. Divide the coefficent of the x term by 2 and square the result.
4/2 = 2
2² = 4

3. Add and subtract the result from step2 inside
the brackets [you just "completed the square"]
y= 3(x² + 4x + 4x -4x) -5

4. Factor the first three terms in the brackets into
a perfect square.
y= 3[(x+2)² -4] -5

5. Distribute the number outside the brackets.
y=3(x+2)² -12 -5

6. Simplify
y=3(x+2)² -17

*Sinusoidal Graphs:
F(x) = AsinB(x-C) + D or F(x)= ACos B(x-C) + D

The Basic Function Graphs:












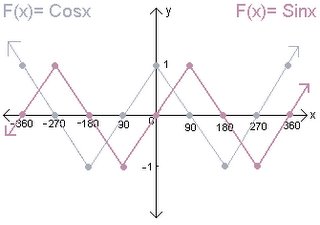
The Role of Parameter A:
/A/ is called the Amplitude or the "vertical strecth." It tells you the distance from the sinusoidal axis to the maximum or minimum value.

The Role of Paramere B:

www.flickr.com

This is a Flickr badge showing public photos from Flickr tagged with pc30sf06. Make your own badge here.

Check out the entire collection!