From Natnael .... To Pre-cal30sf06

Hey guys,

This is my last scribe post on this blog.

I just wanna say a couple of things before i leave from Winnipeg. I really loved this class, and all of you guys. This was such an awesome experience for me, an dam sure for a lot of you. It was such a short time, and this class really kinda got us together on math. I've rarely done math with friends, i usually do it just individually, which i don't think i will continue doing, because of what i saw in the class.

Oh about the postcard... guys ... really THANK YOU V.V.V.V.V.V.MUCH ... and Sam... i will try not to find friends better than you ;[]:...

This class was such an amazing class i think. we all cooperated and worked together till the last minute (be4 the exam) Everyone was blogging, and sharing what he/she knew.. it was awesome.

Well, guys, wish if i had staid with you guys longer.. at least till grad, but u know i have to move.. i guess if God wills we will get together sometime (theres a .009 chance..).

Mr. K. you've been a wonderful teacher of the course, i really liked the way you would put examples on the board.. the pretest... the quizzes.. almost every thing.

Hope you guys enjoy your upcoming academic years. AND EVERYONE IN THAT CLASS SHOULD STICK TO PRE-CAL, and i really do wish everyone good luck!!.. and am sure all of u will.

Well its so sad, but.. this might be my last time talking to you guys...so good bye... in case anyone wanna add me to his/her msn this is ma email nathaniel_td@hotmail.com


Bye

Natnael

Functions

Function: Functions are set(s) of rules that turn one mathematical object into another.

FUNCTIONS + RELATIONS

-All functions are relations.
-Not all relations are functions.

Four ways of presenting functions: [Using the function f(x) = x + 1]

1) Verbal
...the input changes to an output after adding one unit to it.
2) Graphically: Graph

3) Numerically: Table of Values

4) Symbolically: Equation
f(x) = x + 1

FLAVORS OF FUNCTIONS

1)Many-to-One Function

This is when a function provides one output for two or more inputs.

in the above example; when the input is -2 the output is 3.5, and when the input is 2 the output is 3.5 again.

2) One-to-One Function:

This is a kind function, where there's is only one output for one input.
E.g f(x) = x - 3

FUNCTION COMPOSITION

Function composition dimply means: feeding a function into another.
for e.g.
Note: We can use all the operations on function compositions.

TEST FOR FUNCTIONS:
This is done by the vertical line test, which ensures that there's only one output for each input.
e.g. 1\ Passes 2\ Fails

Direct and Indirect reasoning

Good evening everyonethis is m@rk scribing for yesterday's class. I've been banged up by high fever that is why i was unable to go to class today.

To start yesterday's class we proved using direct reasoning that the product of 2 even numbers is even too.First of all an even number is something that is divisible by 2 and has a factor of 2.

Let 2x=an even number
2a=another even number

2x * 2a =4ax
2x * 2a= 2 (2ax)

∴ Any product by both even numbers is also even as seen from above.

Then, we proved using direct reasoning that the product of 2 odd numbers is odd too.

Let (2x+1) =an odd number
(2a+1) = another odd number

(2x+1) (2a+1) =4ax+2x+2a+1
(2x+1) (2a+1)=2 (2ax+x+a) 1

∴ Any product by both odd numbers is also odd as seen from above because the product does not factor perfectly with 2.

Now, from the previous class we proved that √2 is irrational using indirect reasoning.

First, assume that √2 is rational.

√2=a/b

Note: a/b is in reduced form meaning they have no common factors.

2= a²/b² Multiply both sides by b²
2b² =a²

a² must be an even number and a must be even too so, let a=2c.

2b² = (2c)²
2b²=4c²
b²=2c²

b² and b are both even numbers so, let b=2d. This is a contradiction! Both a and b cannot have any common factors because of our assumption that they are in reduced forms in the beginning.

∴ √2 is irrational

Then, we prooved that √3 is irrational using indirect reasoning.

First, assume that √3 is rational. THis problem is similar to the the previous one.

√3= a/b

Assume that a/b is in reduced form.

3= a²/b²

3b² = a²

On the other hand lets look at square numbers first.
4= 2*2
9=3*3
16=2*2*2*2
25=5*5
36=2*3*2*3
49=7*7
64=2*2*2*2*2*2
81=3*3*3*3
100=5*2*5*2

Can you see the pattern that there is always a pair of prime numbers in square numbers?

So let b²=3c

3(3c)² =a ²

3* 9c² =a²

BUt it cannot happen because a and b will share the same factor which is 3. Therefore contradicting with our first statement that a and b is in reduced form.

∴√3 is irrational

Lastly, we talked about pardoxes. A paradox is a statement that cannot be true but also cannot be false.

Example:
This sentence is false

In this case you cannot decide whether it is true or false.

Thats it for my scribe for tonight. I dont know if im going to be able to go to class tomorrow. It all depends if im feeling better . LIke i told Mr. K the scribe will be Natnael. The homework is the Unusual school play

LOGIC

Salutations fellow classmates,

Today in class, for all you naughty kids that skipped (haha jk), we kind of had a work period. Mr. Kurropatwa had to leave for some meeting, but before that, he had handed out the Go For Gold assignment, which is to be due in about 2 weeks from now.

Rules for Go For Gold:
1) only two options for marks; zero or one hundred.
2) you may talk to other students.
3) you can ask Mr. K ONLY one question.
4) you must complete it and hand it in on time. (it IS a good way to prepare for the exam)

He also handed out the second consumer math booklets. We only got one worksheet to fill in for now and the other worksheets will be handed to us tomorrow. Tomorrow's not a good day to skip then ;)

He also told us that our other project is up and running, the wiki. There will be enough questions for at least everyone to do. Here's the link to it: www.pc20sf06.pbwiki.com
Our photo trigonometry projects are due today and we received our rubric on how we're being marked.

Throughout the class, we all worked on our Go For Gold. Hopefully everyone does well on that, and we all get 1 hundred! Remember to work on the wiki and to go to class tomorrow because we get our worksheets (and who doesn't like to get an early start on work? lol). Yeah, and that's about it. Our next scribe for tomorrow will be

...............................................................................
...............................................................................
...............................................................................
...............................................................................
...............................................................................

LAURESSA!!! :D

New Year With Continuation of Last Year's Class

Hi and happy new year everybody and I hope you all had a great holiday. Today we continued on what we left off on the last day of school before the holidays. We worked on some word problems that had to do with Venn- Diagrams. These are the questions:

1. Recently several DMCI students were surveyed about their favourite music groups.
The results were:

• 22 like Hole
• 25 like U2
• 39 like Third Eye Blind (TEB)
• 9 like U2 & Hole
• 17 like Hole & TEB
• 20 like U2 & TEB
• 6 like all three
• 4 like non of these three

a) How many students were surveyed?
b) How many students liked U2 only?
c) How many students like exactly 2 groups

2.Every year over 9 million tourists visit Turkey. Last year 9.8 million tourists vistited Turkey.

• 60% visited only Istanbul
• 20% visited Izmir
• Half of the tourists who visited Izmir also visited Istanbul
• 2% visited Istanbul, Izmir, and Antalya
• The number of tourists who visited only Antalya was half again as much as the number of the tourists who only visited Izmir
• Tourists who visited Antalya either saw only Antalya or Antalya, Istanbul, and Izmir
• The rest of the tourists visited other regions

How many tourists visited other regions?

Solutions
1.So first we fill in a three circle venn diagram because there are 3 different groups.
I'll explain the diagram, first we work our way from the middle and we know that there are 6 people who like all three groups. Now we pick one of the next 3 overlaps and find those. Lets use U2 & Hole as an example, we know from the clues that 9 people liked Hole & U2 so we subtract 6 from the 9 because the 6 represents 6 people that also like Hole & U2. So we have 3 in that section. Once those sections are complete we work on the outer sections. Like the overlaps we take the total number of people that like that group and subtract the number of people that like that group and other groups also.

a)This question asks us to find the number of students survey, so we just add all the numbers up and we get 50

b)This question asks us to find the number of students who only liked U2 and the answer is 2 according to the graph

c)This question asks us to find the number of students who like only 2 groups and the answer is 28. We get that by adding the numbers that are in the section of 1 overlap which are 3, 11, 14.

2.This quest is a doozy because we have to go back and forth with the clues.


This album is powered by
BubbleShare
- Add to my blog

If the pictures are going too fast, feel free to pause or replay.

• The first picture shows inserting the info from the first clue and from the clue it tells us that 60% of the total tourists visited only Istanbul. We can put it on the venn diagram because the clue states that 60% visited only Istanbul.
• The second picture shows the third clue and with the second clue in mind we can find the Istanbul- Izmir overlap because the clue states that half of the number of tourists that visited Izmir also visited Istanbul. So half of 20% is 10% and that leaves us with 10% for Izmir.
• The third picture shows the addition of the middle section with the forth clue.
• The forth picture shows the sixth clue which states that the people who visited Antalya only visited Antalya or saw all three places and not 2 places. So we know that the Izmir-Antalya and Istanbul-Antalya sections have 0%'s. And now we can find how many people visited Izmir and it is 8% because before we had 10% and due to the forth cluwe are left with 8% and that 8% go into the Izmir section.
• The fifth picture shows the fifth clue and it states that the people that visited Antalya is equal to 1.5x the number of people who visited Izmir and 8 x 1.5= 12. So Antalya is 12%.
• The final picture shows the addition of the last clue which states that the remainder of the tourists visited other regions.

To answer the question we need to know the number of people who visited Turkey and the percentage of the tourists who visited the other regions. To find the number of people who didnt visit Istanbul, Izmir, and Antalya we take the total number of tourists multipied by the "other" percentage in decimal form.

After the explanation of those two questions we began with a new logic subject.
Mr. K told us to take out a new piece of loose leaf and draw the biggest circle you can draw on that paper and make a dot on the circumference. Then he asked us how many different flat areas there are in the circle and there are 1. He told us to make a second dot and connect the dots and asked us how many areas are there and there were 2. Then a 3rd dot and then connect that dot with every other dot and then do the same as before and there were 4 areas. Now look at the graph.
This album is powered byBubbleShare
- Add to my blog


So lets think of an equation to helps us find the number of areas if the number of points is 457.
As a class we discovered that the equation 2^(n-1) where n is the number points will work. So we tried the equation with 6 as the number of points and using the equation we predicted the number of areas will be 32. Now continue with the diagram with 6 dots and count the number of areas. Oh no there is only 31. That is situation called a counterexamples and that is when there is a theorem made and there is one example that doesn't fit the theorem. That just makes the theorem a theorem that is not true. Tomorrow will be the continuation about counterexamples.

Okay that was our first class back from the holidays and it was kind of tiring to go back to school after a 2 week break. Homework (homework*sigh*) is exercise #48 and it is about counterexamples.

The next scribe will be SAMUS!!!
Good Night :-)

" L O G i C " - cont'd

To start off today's class, we were given a few reminders:

• FLICKR.com RUBRIC: Reminder to students that this is for your benefit. Putting in your voice nto this document will affect how your flickr assignments are graded. This document should be about how you want your assignments to be marked, and how the assignments should be done. Get crackin'!
  



• NEXT FLICKR ASSIGNMENT: The next flickr assignment will be to take a picture of TRIGONOMETRY. Be unique and creative and find a photo no one else will have. This won't be due until the first tuesday after winter break. We'll be given a great amont of time for this assignment, but don't procrastinate!
  
  Today, we added in some more notes into our math dictionary:

Here are a few examples of some arguments:

Example 1 and 2 both are true and valid statements. The reason being the premises of each example makes sense with what the conclusion says. The conclusion makes sense of what has been stated and flows naturally. This is called a sound argument.

SOUND ARGUMENT: an argument that is both valid and true.

AN EXAMPLE OF A FALSE ARGUMENT:

"All men are mortal.
Mr. K is a man
... Mr. K wears glasses."

That was a false statement because, even if the three statements alone are true, together as an argument, it's not. The conclusion doesn't flow naturally with the premises, and it doesn't make sense.

**************************************

We also discussed different TYPES OF REASONING that we go over in this unit of Logic:

Induction: When we observe several particular examples that identify a pattern and conjecture that it must always be that case.

EXAMPLES:
QUESTION: Will the sun rise tomorrow?
ANSWER: It has every day before, so it will rise again tomorrow.
*That's the answer because through all the years we've been living, a reoccurring pattern of the sunrise has always taken place.

NOTE: To view more examples of inductive reasoning, look over all the investigations we worked on in our circle geometry unit!

Deduction: When we argue from basic, unarguable truths, to a valid conclusion.

An example of deductive reasoning is the process of proving THALES' THEOREM.

***************************************
In logic, we also look at relationships between different sets, and compare them in Venn Diagrams.
In the following images, we see how sets are made, and how we can compare two different sets using a venn diagram.

***************************************

Weeell ..

TOMORROW'S THE DAY! CIRCLE GEOMETRY UNIT TEST

I HOPE YOU GUYS ENJOYED MY SCRIBE..

blogger was being a pain in the behind and erased my

first draft and I had to start all over again!

BUT, I DID IT AGAIN. YET ANOTHER SCRIBE POST BY ME!

TOMORROW'S SCRIBE WILL BE ...

M@RK.

(just cuz he told me to pick him!)

NiGHT!!

New Unit: Logic

So today we started logic which is a system of reasoning or the way you present an argument.

Mr.K asked us if the sun is going to rise tomorrow and if i'm not mistaken almost everyone thinks that the sun is going to rise tomorrow based on the fact that the sun has been setting and rising every single day of our lives so far. That brings us to inductive reasoning and deductive reasoning

Inductive reasoning is when you come up with a hypothesis based on examples or observations to make a general rule more specific.

Deductive reasoning is when you use fundamental trues to create a rule. An example of deductive reasoning is Thales' theorem.

Something like this would be inductive:

Draw the next two.
With the next two it would look like this:


Something like this would be deductive:

Draw the next figures.
There really is no right answer for this question, you can look for a pattern but you must explain 3 things: the square, the curve, and the dot.


Here is a true or false questions:
1. The square of a number is larger than the number.
- this is false because the square of 1 is not larger than 1 (1² = 1)

A sentence like "This sentence is false." is what we call a paradox. It is true and false because it refers to two things at the same time and it is a self-reference.



valid means it flows natuarally from the premisis.
invalid means it does not flow naturally from the premisis.

All men are mortal
Mr.K is a man
Mr.K is mortal
^^ This is what we call a sound argument because it is both true and valid

A few examples of unsound arguments are:
All men are squibbles
Squibbles are pink
All men are pink
^^ This is unsound because it is valid but it is false.

All men are mortal
Mr.K is a man
Mr.K wears glasses
^^ This is unsound because it is all true but it is also invalid

All men are green
Mr.K is a man
Mr.K is green
^^ Something like this is also unsound because it is valid but most of it is false


SO THAT IS WHAT WE DID TODAY. HOMEWORK IS EXERCISE 45
&&
CONSUMER MATH - WAGES ASSIGNMENT **due on friday

NEXT SCRIBE IS LAURESSA

Circle Geometry: Theorem Summary

Okay, so I was responsible in making the first post dedicated to Circle Geometry and now I'm responsible in making the last post dedicated to Circle Geometry. Just like the first post, the following information is the "Dictionary Information."

The usual human brain can only remember at max 7 items, according to Mr. K. In remembering a phone number, we chunk the 7 digits into 2 groups so its easier to remember. Just like remembering a phone number, we chunk all the theorems into 4 categories.

next scribe is crysta! go crysta! i'm sure you'll find some new innovative way for learning just like what u did with that bubbleshare thingy! =)

Circle Geometry - Pretest

Today we did our pre test in class for Circle Geometry. More or less i think the whole class found that the long answer question and the last multiple choice question were the hardest, so i'll explain those. =)


LONG ANSWER
Determine the measure of ےECB, ےBDC, ےBAD, and ےDBE, where E is the centre of the circle.

So first of all we always start with a table that has STATEMENT on one side and REASON on the other.

It's obvious at this point that BE and CE are radii, therefor triangle BCE is an isosceles triangle. This also means that ےEBC and ے BCE are the same.

NOTE: CLICK ON BUBBLESHARE BOX TO SEE FULL EFFECTS. =)

We now know the exact amount of ےBCD and according to cyclic quadrilateral theorem ے BCD's and ےBAD's sum should equal 180°. So in order to find ےBAD, we subtract 30° and 40° from 180° and come up with 110°. Therefore ےBAD is 110°.


Another thing we looked at were the two triangles that are subtended by the same arc; triangle BCE and triangle BCD. Since all of us know of the central inscribed angle theorem ( AKA the star trek theorem ) we can easily point out that ےBDC is half the amount of ےBEC. As a result ےBDC = 100°/2 which equals 50°.


We only have one angle left! Angle DBE! So if we look closely at triangle BCD you'll realize that we only have one angle left to find, ےDBE. We also know that every the angles of a triangle sum up to be 180° and by subtracting every angle that we have we'll be able to come up with the value of ےDBE! :D

Which in this case in 20°! =)

Once you've found your information and proofs, your table (including "Statement" and "reason") should look something like this:



MULTIPLE CHOICE
In the diagram below, R, S, T, U are points on the circle with RS = RU = UT and SU = ST. Find the measure of ےUST.
a) 31°
b) 35°
c) 36°
d) 40°
e) none of these


The first thing you should always do is mark down what is given to you. Have a wishful thinking colour, a colour used for given facts and a colour used for things you have proven! ( it comes in handy :D )
I'll use purple as the facts that are given, blue for what we're looking for and orange for the facts i prove. =)

There's no particular order to do this in, but what i looked at first was the isosceles triangles. We can easily point out that ےRSU and ےRUS are the same and ےSUT = ےSTU.


Now if we look at RS, RU and UT they are all the same length. Which means that the angles subtended by this chord length will all be the same. SOOO.. ےRST = ےRUT = ےUST.


In order to find the exact degree that angle is we make three equations. (this is like going back to substitution in linear equations). Here are the three equations (let ےSRT = w):
1. w + z = 180
2. 3y + z = 180 --> z = 180 - 3y
3. w + 2y = 180 --> w = 180 - 2y

If we substitude 2 and 3 into 1, we can find out what Y is, which is ےUST.
180 - 2y + 180 - 3y = 180
180 + 180 - 180 = 2y + 3y
180 = 5y
36 = y

And there you have it!
c) 36° is the correct answer. =)


That's all for tonight! Sorry for the late entry, i had to go and watch my brother's christmas concert! haha. =) Well, no homework tonight, just study! Test tomorrow. Good luck guys!

HAPPY HOLIDAYS! =]




And the next scribe will bee..... -Zeph! Enjoy. =)

Test Prep Exercises - Questions 1, 2 and 8

hey guys. Sandy and I had an agreement to switch days, if she chose me tomorrow.
So yes, its me EEDCE.



(1) In the diagram below, AB and CB are tangents to a circle with radius 10. If angle AB find x, the shortest distance from B to the circle.

cos50°=10/h
h = 10/cos50
h = 15.557units

x = h - 10
x = 15.557 - 10
x = 5.557 units

(2) Given: Circle with centre C
- Angle 1 = Angle 2
Prove AB=CD

statement proof
Angle 1 = Angle B given
BC ~= CD ~= AC radii
Triangle ABC is isoscles from above
Triangle ACD is isoscles from above

Therefore, AB cannot be congruent to CD.





8. Complete the proof:
Diagram clarification: E, D, C are collinear
Given: EA is tangent to the circle at A
AB EC

Statement Proof
AD // BC given
EA is tangent at A given

Angle 8 = Angle 7 Tangent-Chord Theorem
Angle 7 = Angle 5 Alternate Angles
Angle 6 = Angle 8 - Angle 9 Tangent-Chord Theorem
Angle 1 = Angle 2 Triangle ABC ~ Triangle AEC








Okay. thats it folks.
homework is to finish the rest of this pre-test if not yet done so.

SANDY will take it away tomorrow.

Circle geometry

Salutations fellow math students,

Today, for all you naughty kids that skipped (haha jk), we worked on five different circle problems that Mr. K had put up for the class to do. They were:

1) A chord that is 10cm long is 12 cm from the centre of a circle. Find the radius.












2) Line AB and line CD are two parallel chords in a circle. Line AB is 10cm and Line CD is 14 cm. Find the radius if the chords are 3cm apart.














3. a) O is the centre of each circle. Find the measures of the indicated angles. Justify your answer.


















3. b)

















4) Given:
-Line AC is tangent at B
- Angle 1 is congruent to angle 2

Prove: Line BD // Line FC



















So yeah that's what happened in class. Homework was posted up on the blog by our very own math teacher, Mr. K. And I choose........................................................................................SANDY cheeks to be our scribe for tomorrow's class.

Math Dictionary, Circle Geometry

This album is powered by
BubbleShare
- Add to my blog

I will add the last bits of info. left in the dictionary later...for now, the next scribe will be Samus.

Investigation 10. Angle sum of Polygons

Circle Geometry - Investigation 8

Good evening everyone. Today Mr. K talked to us about our flickr photo assignment at the beginning of class. The due date is now on Monday. Just a little reminder for you all.

We did investigation 8 today. Here were the instructions.

1.

(a) Construct a chord AB in the circle.
(b) Construct a tangent, RS, to the Circle at A. The tangent should not be perpendicular to AB.
(c) Measure the angle of RAB.


This album is powered by
BubbleShare
- Add to my blog


You can plot down the points anywhere you'd like. Just be sure that your chord and the tangent line aren't perpendicular. I measured angle RAB and ended up with 35° with mine.

(d) Construct a point, C, on the circle, on the opposite side of chord AB from angle RAB.
Some of us where have a few problems plotting down C. We did plot C opposite of the chord AB, but had it plotted down inside the circle. The question asks to plot it on the circle, meaning on the circumference. What we did was plot it down in the circle which was different from what was being asked. So, just look out for those small things and read the question carefully.

(e) Construct and measure inscribed angle ABC. What do you notice?
From looking at the slide below, you will notice that angle ACB is the same as RAB.


This album is powered by
BubbleShare
- Add to my blog


(f) Measure angle SAB.


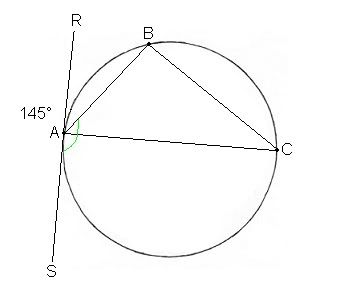
As you can see, angle SAB measures 145°.

(g) Construct a point, D, on the circle, on the opposite side of the chord AB from angle SAB.
(h) Construct and measure inscribed angle ADB. What do you notice?


This album is powered by
BubbleShare
- Add to my blog

Angle SAB and ADB are the same.

Here is sort of a final drawing on all the angles that were measured.



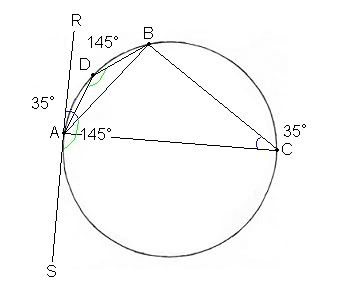
THIS HERE IS CALLED THE TANGENT-CHORD THEOREM.

(i) Can you articulate a general rule for what you have found? Your sentence should begin:
"If an angle is formed between a tangent line and a chord, then...."

The rule here is simply that "If an angle is formed between a tangent line and a chord, then the inscribed angle subtended by the opposite side of the chord is congruent."

RULE
IF AN ANGLE IS FORMED BETWEEN A TANGENT LINE AND A CHORD, THEN THE INSCRIBED ANGLE IS SUBTENDED BY THE OPPOSITE SIDE OF THE CHORD IS CONGRUENT.

And yes, I did mean to repeat that, and repeat it in a way that will be easily read. It's so that you can remember the rule better. Through repetition. Hopefully it works.

The HOMEWORK for tonight is to Re-do the questions we had trouble with in EX. 33. And also EX. 34.

REMINDER: There will be a quiz maybe tomorrow, or the next day after.

I chose the next scribe to be Natnael.

Good Night~

Today's class we started off by handing in our projects. I hope everyone gets over 80% just like Mr. K said we should.

After that he showed us some examples of the 40s student's trigonometry pictures, so have a better clue of what to do with our quadratic function pictures. Make sure it has a lot of details a quadratic function should have.

*Reminder it should be uploaded on flickr by Thursday.

We went over some question in our exercise #32 which were # 10, 12, 13

#10 was a question that didn't really fit in with any unit we did so far but it was a fun question to solve.

#12 this question we had to find the ticket price that will yield maximum profit.
This is a good review for our Analytic Geometry unit.

revenue = (# ticket) (cost/ticket)
let x = 1 discount of $3.00

R (x) = (1000 + 100x) (60 - 3x)

roots @ x= -10 x= 20

We ended up with the price $45 per ticket.

#13

A) y= x and y = -1/2x+2

B) x=-1/2x+2
2x=x+4
3x=4
x=4/3

(4/3, 4/3)

C) 8/3


After going over some homework we started on our Investigation #7


This album is powered by
BubbleShare
- Add to my blog


"If two tangents are drawn from a common point, exterior to a circle, then...the tangent lines are the same measure"

"If a radius intersects a tangent line, then...the angle is 90 degrees"

After all of that the next step is to go back and construct a new point S exterior to the circle and repeat steps b, c and d for point S.

Today's homework is exercise #33
Make sure to attempt every question. The ones you are really stuck on should be looked at in class.

And most of you may notice that the scribe list is now on our fourth cycle!! that's a lot of scribing!. I just wanted to say I'm really proud of every one's work. Look how far we came with our scribing, we're using a lot more tools to make our post explained to the best of our abilities.

Okay enough of that...the next scribe for Wednesday (Tuesday afternoon NO SCHOOL!) is... MERIAN!

GOOD NIGHT!

Circle Geometry!

To start off today's class we all congratulated Crysta on her Fantastic! scribe post. Once again, great job Crysta! Mr. K was also trying to explain to us the meaning of how much one million (1000000) really is. If we broke it down to how long it would take to reach one million by receiving one penny each second. When we finished calculated it, it took 11.5 hours. Then we decided to calculate how long it would take to reach a billion (1000000000). We all found out that it would take 32 years to reach that. We also realized that we haven't even lived for a billion seconds yet AND one billion penny's will fit into 5 school buses. Quite interesting, don't you think? If you're wondering how Mr. K knew all this, he went to this website

http://www.kokogiak.com/megapenny/

Anyway, once we got back onto to track we discussed questions that we had trouble with from last nights homework and we did Investigation 5.

(a) Choose 6 different points on the circumference of the circle. Do not space them out evenly. Label these points A, B, C, D, E and F.
So this part is pretty straight forward. We start with a blank circle and add 6 points anywhere on the circumference.

This album is powered by BubbleShare - Add to my blog

(b) Construct angles ACB, ADB and AEB.
For this part of the investigation, we're pretty much making chords, but these are to make angles.

This album is powered by BubbleShare - Add to my blog

(c) Measure the angles formed at C, D and E.
So here we take the angles and measure them. It's best to write them down that way we can keep track of them. instead of just adding it to the picture.

This album is powered by BubbleShare - Add to my blog

When I completed this step in class, i got this:
ACB = 13°
ADB = 13°
AEB = 13°
Notice a pattern?

(d) Construct angles EAF, EBF and ECF.
Here, we will repeat what we did for (b).

This album is powered by BubbleShare - Add to my blog

(e) Measure the angles formed at A, B and C.
Here we'll do the same as (c).
EAF = 60°
EBF =60°
ECF =60°

(f) What do you notive about all these angles? Can you articulate a general rule for what you have found? Your sentence should begin:
"If two (or more) inscribed angles are subtended by the same arc, then..."
Have you seen the pattern to these? Well, If you have you've noticed that all the angles come out to equal the same. To complete the sentence can be said in different ways.
i) ... they have the same measure.
ii) ... are congruent
iii) or in your own words!

So there you have it! investigation 5! I don't know if it's just me but these things are super fun to do. haha. (:

Anyway. Homework for the weekend is:
1. Attempt to complete Investigation 6. (but if you get frustrated with it, then leave it be)
2. Exercise 31.
3. Project (due monday)
4. Picture of a parabola put onto Flickr. (due thursday)
REMEMBER TO DO YOUR HOMEWORK, GUYS. =)

As for the next scribe.. i think** the only person left is MELISSA! .. haha. if i'm wrong, correct me, otherwise, Have a great weekend!

Okay so i didn't get to do my post when i was scribe last time cause my net wasn't being very nice. Today in class we did investigations 3 and 4.

Investigation 3:
1.(a) Use what you know about chords to find the centre of the circle. Erase all construction lines once you're done.

This is how you do question 1.(a) (If you do have any questions, this question is explained in the previous scribe):

This album is powered by
BubbleShare
- Add to my blog

(b)Construct diameter AB.

Heres what you do:

This album is powered by
BubbleShare
- Add to my blog

(c)Choose 4 different points on the circumference of the circle. Do not space them out evenly. Label these points C, D, E and F.

This questions is self-explanatory:

This album is powered by
BubbleShare
- Add to my blog

(d)Construct chords AC and BC.
(e)Measure the angle formed at C

Draw lines from A to C and from B to C and measure the angle C:

This album is powered by
BubbleShare
- Add to my blog

(f) Repeat steps (c) and (d) for the points labeled D, E and F.

It's pretty straight forward:

This album is powered by
BubbleShare
- Add to my blog

(g) What do you notice about all these angles? Can you articulate a general rule for what you have found? Your sentence should begin:
"If an inscribed angle is subtended by a diameter then...."
If an inscribed angle is subtended by a diameter then.... the inscribed angle is always 90°.

So that was Investigation 3. We started Investigation 4 but did not get a chance to go over it in class. THE SCRIBE FOR THE WEEKEND IS .. SANDY !

Dictionary

For those of us who missed out on our math dictionary I'll fill you in.
Well it's actually just the end of what we couldn't finish yesterday.

• Being able to find the root sum and root product of f(x)=2x^2-6x+7

A=2 Root sum= -b/a Root product= c/a
B=-6
C=7 -(-6)/2 = 3 7/2

• Find a quadratic function whose sum is -3 and whose product is 5/2
  
  Root sum= -b/a Root product= c/a
  -3/1 = -b/a 5/2= c/a
  
  -6/2 = -b/a both must have a common denominator 5/2= c/a
  

a=2 f(x)=2x^2+6x+5
b=6
c=5

Circle Geometry

Well where should I start. In class we were given our first assignment in class, it wasn't hard but it was relatively new to some of us. Investigation 1 and 2 were our given assignments and here are completed ones in case anyone didn't quite get it .

INVESTIGATION 1
A- Construct 4 different chords (a straight line joining two points on the circumference of a circle), AB ,CD, EF, and GH

• But none of them should be diameters (longest possible chord in a circle that passes through the center) nor should they be parallel. The 4 different chords are in black
  

B- O is the center of the circle. Construct lines from the center that are perpendicular to each of the chords. AB, CD, EF and GH. Label the new points where the new lines meets W, X, Y and Z , The perpendicular lines will be in red . The perpendicular lines are also known as bisectors, because they cut the chord into two.

C- Measure the lengths of the AW and BW. Do so with the rest so every chord has two measurements on either side of the perpendicular line

D- Now after your picture is drawn you should see a relationship between a chord and their perpendicular line.

A LITTLE HELP: "A line perpendicular to a chord, that passes through the center of a circle, the chord."

Here is an example of what your drawing should somewhat look like

INVESTIGATION 2
A- Like the A in Investigation 1 construct 4 different chords AB, CD, EF and GH

• Remember none of them should be parallel to each other nor be diameters
  

B- Construct perpendicular bisectors for each chord. Each bisector should be a chord.

KEY: the way to find the bisector is to measure the chord, and find the midpoint. At that midpoint line up a triangle from your geometry set to make a 90 degree angle and draw the perpendicular.

C- What do all the bisectors have in common? Well once your done they should all intersect at the same point.
D- What can you say about any perpendicular? You could say that the perpendicular bisector of any chord will always dissect the center of the circle.

This diagram should give you an idea of how it should look


Example: chord AB. Length of chord divided by two = point where bisector should cross

To complement our learning we also learned some definitions to go along with our new unit
Bisect- to cut into two exact equal halves
Subtend(subtended)- to hold arms of an angle open by an arc

Well that's it thats all folks
Oh yea before I forget

Share the kindness and leave some kind comments on our friends blog in Scotland
If you forgot the address its exc-el.org.uk/blogs/s3srcibeposts, I checked it out and its pretty neat!


Ex 30 for homework.
NEXT will be ......................Crysta!

Zeph's Notebook/Dictionary: Algebra

just to make things a bit organized, this scribe post is divided into two post. one section will be the circle geometry notes we took and the other post will be the algebra notes. this is so that this scribe post doesnt end up having the labels, circle geometry and algebra, at the same time.

Note: there is still more algebra notes to come from the next scribe!


REMINDERS:

~ FLICKR/NUMBER ASSIGNMENT - GET MORE PICTURES!! TOTAL OF 5 ALTOGETHER
~ "LOST IN MATHLAND" ASSIGNMENT DUE THE DAY AFTER TOMORROW!!
~ NO HOMEWORK
~ LAURESSA'S SCRIBE
~ GEOMETRY SET