Well to start things off we had quiz. The quiz was of course on logic, inductive, deductive, valid and invalid questions. A inductive statement is where you have examples and make a generalization and deductive statement is where you have a generalization and produce an example. The part I thought some of us had problems with was determining whether a statement was valid and invalid. Anyways tomorrow might be the logic test so remember to have your BOB's up just in case. Besides the quiz we had a lot of writing to do in our math dictionaries some new and old things.
MATH DICTIONARY
Some definitions
Set: A collection of objects (could be people, things, numbers etc.)
Subset: A collection of objects that consists of some, all or none of the objects in a given set
Example: Consider set A :(1,2,3)
All of the following are subsets of A : (1), (2), (3), (1,2), (1,3), (2,3), (1,2,3),
Note: is called the "empty set" or "null set" but is still a subset of every set
is called the "empty set" or "null set" but is still a subset of every set
Universe (U) : all objects are being considered
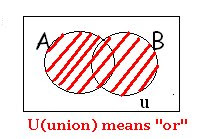
Notation: Union U A U B means gather all objects in set A with all objects in set B

Notation: Intersection
Intersection
 means gather all the objects that are both in set A and B
means gather all the objects that are both in set A and B

- or ' compliment: (reads as " the compliment of A" or "A compliment") means everything outside A
(reads as " the compliment of A" or "A compliment") means everything outside A

 exclusion:
exclusion:  means everything that is in set A but not set B
means everything that is in set A but not set B

Counterexample: Given any logical argument, theorem or hypothesis, if you can find only one case where it is not true, then the theorem or argument is proven false . This is called a "counterexamlple"
Conditional statements: Any statement of the form" If...then..." is called a "conditional" or "implication"
Hypothesis: The first part of the conditional
Conclusion: The second part of a conditional
Example: If(hypothesis) Then(conclusion)
If a triangle is isosceles Then it's base angles are congruent
Well that's all for this scribe and I'll scribe on Friday since I couldn't get my post up in time.
Homework is Ex. 48
Flickr assignment due this Friday
Go for Gold due Wednesday before exam
and our 2nd consumer packet

Set: A collection of objects (could be people, things, numbers etc.)
Subset: A collection of objects that consists of some, all or none of the objects in a given set
Example: Consider set A :(1,2,3)
All of the following are subsets of A : (1), (2), (3), (1,2), (1,3), (2,3), (1,2,3),

Note:
 is called the "empty set" or "null set" but is still a subset of every set
is called the "empty set" or "null set" but is still a subset of every setUniverse (U) : all objects are being considered
Notation: Union U A U B means gather all objects in set A with all objects in set B


Notation:
 Intersection
Intersection means gather all the objects that are both in set A and B
means gather all the objects that are both in set A and B
- or ' compliment:
 (reads as " the compliment of A" or "A compliment") means everything outside A
(reads as " the compliment of A" or "A compliment") means everything outside A
 exclusion:
exclusion:  means everything that is in set A but not set B
means everything that is in set A but not set B
Counterexample: Given any logical argument, theorem or hypothesis, if you can find only one case where it is not true, then the theorem or argument is proven false . This is called a "counterexamlple"
Conditional statements: Any statement of the form" If...then..." is called a "conditional" or "implication"
Hypothesis: The first part of the conditional
Conclusion: The second part of a conditional
Example: If(hypothesis) Then(conclusion)
If a triangle is isosceles Then it's base angles are congruent
Arguments of the form"if..then..." and related statements
A sentence that says only one thing is called a "declarative sentence"
Well that's all for this scribe and I'll scribe on Friday since I couldn't get my post up in time.
Homework is Ex. 48
Flickr assignment due this Friday
Go for Gold due Wednesday before exam
and our 2nd consumer packet



Hi Lauressa,
ReplyDeleteI found this scribe very helpful as I strive for a deeper understanding of math!
Thank you!
Lani