Okay so lets start with Monday. On Monday we started off the class by dividing:
Divide. Indicate any remainders as a fraction.

So question 1 had no remainders but number 2 did have a remainder of 2.
The quotient of question 2 can also be written as 712/3.
Question 3 had no remainder but the quotient can be simplified to 2x2+5x+3=(x+1)(2x+3).
Question 4 has a remainder like question number 2. it can be written as x3-4x2+2x-1=x2-2x-2-5/x-2
Instead of doing division the long way, we learned how to do synthetic division. This is what synthetic division looks like:

On Tuesday we started off the class by finding intercepts.
Find all intercepts
f(x)=4x3-7x+3
*The degree of the polynomial determines the maximum roots that the graph will have. Something like 4x4 could have up to 4 roots.
The first thing you do is find all the possible numerators (you can do this by finding all the factors of the constant in the equation):
±1, ±3
The next thing you do is find all the possible denominators (you can do this by finding all of the factors of the leading coefficient):
±1,±2,±4
From that you can find all the possible roots:
±/1, ±3/1, ±1/2, ±3/2, ±1/4, ±3/4
The easiest way to test if these are roots is by synthetic division:

If there is no remainder, which in this case there isn't, you take the linear factor (x-1) and add the x2 and the x where they belong then multiply the 2 to get the equation of the line.
f(x)=(x-1)(4x2+4x-3)
You can factor this further:
f(x)=(x-1)(4x2+4x-3)
f(x)=(x-1)[4x2+6x-2x-3]
f(x)=(x-1)[2x(2x+3)-1(2x+3)]
f(x)=(x-1)(2x+3)(2x-1)
From here you conclude that there are roots at (1,0), (1/2,0), (-3/2,0) and the y-intercept is at 3 because if you substitue 0 in for x in the equation, you are left with 3.
To draw the graph of this function, you must do a sign analysis. You must substitute numbers between the roots into the equation to check if they are negative or positive. The end result for this equation looks like this:

*The only way a root can change its sign is by passing through zero.
The graph of this function would look something like this:

On Wednesday we started by sketching the graph of f(x)=-2x3-7x22x+3.
These are the steps you take to graph this polynomial:
1.Factor everything
2.Find the y-intercept
3.Find the roots (You may use the roots theorem)
4.Do a sign analysis
5.Sketch the graph
This polynomial is easy to work with in this form.
The y-intercept is the constant which in this case is 3.
Find the roots by finding the possible roots and use synthetic division to find a root:

From this, you can also find points on the graph by using the possible root as the x-coordinate and the remainder as the y-coordinate. Here you have points at (1,-8), (3,-57), and a root at (-1,0)
You can factor the polynomial to find more roots by using the linear equation x+1 and multiplying it by the equation you got by using synthetic division:
f(x)=(x+1)(-2x2-x+3)
f(x)=(x+1)(-2x2-6x+x+3)
f(x)=(x+1)[-2x(x+3)+1(x+3)]
f(x)=(x+1)(x+3)(-2x+1)
From this you get roots at x=-3,-1,1/2 and you can sketch the graph of the polynomial. The graph would look something like this:

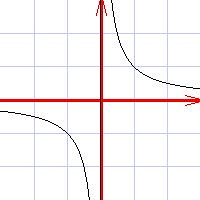
Now something like y=1/x would have a vertical asymptote on the y-axis and a horizontal asymptote on the horizontal axis. The graph would look like this:
The next scribe is eeDce
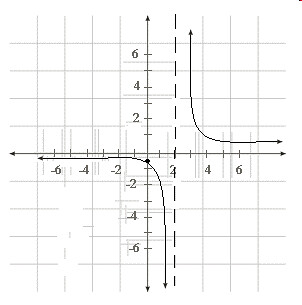
The steps to graphing a function like f(x)=1/x-2 would be:
1.Factor everything
2.Find the y-intercept
3.Find the roots
4.Find the vertical asymptote
5.Find the horizontal asymptote
6.Do a sign analysis
7.Sketch the graph
f(x)=1/x-2 is already factored
The y-intercept would be at y=-1/2
There would be no roots
The vertical asymptote would be at x=2
The horizontal asymptote would be found like this:
limx®¥ 1/x-2
limx®¥ (1/x)/(x/x-2/x)
limx®¥ (1/x)/(1-2/x)
=0/1-0
The horizontal asymptote would be at y=0 on the y-axis. An easier way to find the horizontal asymptote is by taking the leading coefficient of the denominatior and divide it by the leading coefficient of the numberator but only if they have the same degree.
The sign analysis would look like this:

The graph for this would look like this:
THE NEXT SCRIBE IS eeDce

No comments:
Post a Comment