Hey guys,
This is my last scribe post on this blog.
I just wanna say a couple of things before i leave from Winnipeg. I really loved this class, and all of you guys. This was such an awesome experience for me, an dam sure for a lot of you. It was such a short time, and this class really kinda got us together on math. I've rarely done math with friends, i usually do it just individually, which i don't think i will continue doing, because of what i saw in the class.
Oh about the postcard... guys ... really THANK YOU V.V.V.V.V.V.MUCH ... and Sam... i will try not to find friends better than you ;[]:...
This class was such an amazing class i think. we all cooperated and worked together till the last minute (be4 the exam) Everyone was blogging, and sharing what he/she knew.. it was awesome.
Well, guys, wish if i had staid with you guys longer.. at least till grad, but u know i have to move.. i guess if God wills we will get together sometime (theres a .009 chance..).
Mr. K. you've been a wonderful teacher of the course, i really liked the way you would put examples on the board.. the pretest... the quizzes.. almost every thing.
Hope you guys enjoy your upcoming academic years. AND EVERYONE IN THAT CLASS SHOULD STICK TO PRE-CAL, and i really do wish everyone good luck!!.. and am sure all of u will.
Well its so sad, but.. this might be my last time talking to you guys...so good bye... in case anyone wanna add me to his/her msn this is ma email nathaniel_td@hotmail.com
Bye
Natnael
January 30, 2007
January 29, 2007
January 28, 2007
Autograph that final exam and your life with EXCELLENCE!
A BIG THANKS TO LANI!
Dear Lani,
Since our semesters coming to an end, our class and myself personally would like to thank you for your contribution to our blog. You've definately added to our learning experience and your advice will be with us always. To think you took time out of your busy schedule to mentor a small group of Pre-cal students in Winnipeg, Manitoba. Mr. K and our class appreciate your time and sincerity. THANKS LANI!! Good day, and have fun!
Since our semesters coming to an end, our class and myself personally would like to thank you for your contribution to our blog. You've definately added to our learning experience and your advice will be with us always. To think you took time out of your busy schedule to mentor a small group of Pre-cal students in Winnipeg, Manitoba. Mr. K and our class appreciate your time and sincerity. THANKS LANI!! Good day, and have fun!
THANK YOU Lani!
Thanks Lani for giving us your support. We gladly appreciate it. You've always been there cheering us on, encouraging us to move forward. I'm sure the class has a lot more to say, but nonetheless, we feel like we owe you a big thank you...
THANK YOU!
~ -Zeph
GO PC30SF06 GO!
THANK YOU!
~ -Zeph
GO PC30SF06 GO!
January 24, 2007
Graphing Functions Notes
As promised, here they are, the full set of notes for graphing polynomial and rational functions. These notes must be copied by hand into your math dictionaries. Do not hand in the printed pages. There is a good reason for this ... if you really want to know ask me in class. ;-)
Learn Hard!
Page 1 of 7
Page 2 of 7
Page 3 of 7
Page 4 of 7
Page 5 of 7
Page 6 of 7
Page 7 of 7
Learn Hard!
Page 1 of 7
Page 2 of 7
Page 3 of 7
Page 4 of 7
Page 5 of 7
Page 6 of 7
Page 7 of 7
Scribe Post
Omg sorry i got mixed up with natnael and melissas post because natnael posted after melissa but yeah i'll do monday, tuesday, and today. Once again sorry for keeping you guys waiting.
Okay so lets start with Monday. On Monday we started off the class by dividing:
Divide. Indicate any remainders as a fraction.

So question 1 had no remainders but number 2 did have a remainder of 2.
The quotient of question 2 can also be written as 712/3.
Question 3 had no remainder but the quotient can be simplified to 2x2+5x+3=(x+1)(2x+3).
Question 4 has a remainder like question number 2. it can be written as x3-4x2+2x-1=x2-2x-2-5/x-2
Instead of doing division the long way, we learned how to do synthetic division. This is what synthetic division looks like:

On Tuesday we started off the class by finding intercepts.
Find all intercepts
f(x)=4x3-7x+3
*The degree of the polynomial determines the maximum roots that the graph will have. Something like 4x4 could have up to 4 roots.
The first thing you do is find all the possible numerators (you can do this by finding all the factors of the constant in the equation):
±1, ±3
The next thing you do is find all the possible denominators (you can do this by finding all of the factors of the leading coefficient):
±1,±2,±4
From that you can find all the possible roots:
±/1, ±3/1, ±1/2, ±3/2, ±1/4, ±3/4
The easiest way to test if these are roots is by synthetic division:

If there is no remainder, which in this case there isn't, you take the linear factor (x-1) and add the x2 and the x where they belong then multiply the 2 to get the equation of the line.
f(x)=(x-1)(4x2+4x-3)
You can factor this further:
f(x)=(x-1)(4x2+4x-3)
f(x)=(x-1)[4x2+6x-2x-3]
f(x)=(x-1)[2x(2x+3)-1(2x+3)]
f(x)=(x-1)(2x+3)(2x-1)
From here you conclude that there are roots at (1,0), (1/2,0), (-3/2,0) and the y-intercept is at 3 because if you substitue 0 in for x in the equation, you are left with 3.
To draw the graph of this function, you must do a sign analysis. You must substitute numbers between the roots into the equation to check if they are negative or positive. The end result for this equation looks like this:

*The only way a root can change its sign is by passing through zero.
The graph of this function would look something like this:

On Wednesday we started by sketching the graph of f(x)=-2x3-7x22x+3.
These are the steps you take to graph this polynomial:
1.Factor everything
2.Find the y-intercept
3.Find the roots (You may use the roots theorem)
4.Do a sign analysis
5.Sketch the graph
This polynomial is easy to work with in this form.
The y-intercept is the constant which in this case is 3.
Find the roots by finding the possible roots and use synthetic division to find a root:

From this, you can also find points on the graph by using the possible root as the x-coordinate and the remainder as the y-coordinate. Here you have points at (1,-8), (3,-57), and a root at (-1,0)
You can factor the polynomial to find more roots by using the linear equation x+1 and multiplying it by the equation you got by using synthetic division:
f(x)=(x+1)(-2x2-x+3)
f(x)=(x+1)(-2x2-6x+x+3)
f(x)=(x+1)[-2x(x+3)+1(x+3)]
f(x)=(x+1)(x+3)(-2x+1)
From this you get roots at x=-3,-1,1/2 and you can sketch the graph of the polynomial. The graph would look something like this:

Now something like y=1/x would have a vertical asymptote on the y-axis and a horizontal asymptote on the horizontal axis. The graph would look like this:

The next scribe is eeDce
The steps to graphing a function like f(x)=1/x-2 would be:
1.Factor everything
2.Find the y-intercept
3.Find the roots
4.Find the vertical asymptote
5.Find the horizontal asymptote
6.Do a sign analysis
7.Sketch the graph
f(x)=1/x-2 is already factored
The y-intercept would be at y=-1/2
There would be no roots
The vertical asymptote would be at x=2
The horizontal asymptote would be found like this:
limx®¥ 1/x-2
limx®¥ (1/x)/(x/x-2/x)
limx®¥ (1/x)/(1-2/x)
=0/1-0
The horizontal asymptote would be at y=0 on the y-axis. An easier way to find the horizontal asymptote is by taking the leading coefficient of the denominatior and divide it by the leading coefficient of the numberator but only if they have the same degree.
The sign analysis would look like this:

The graph for this would look like this:
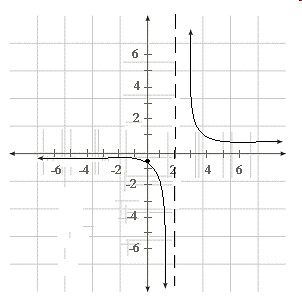
THE NEXT SCRIBE IS eeDce
Okay so lets start with Monday. On Monday we started off the class by dividing:
Divide. Indicate any remainders as a fraction.

So question 1 had no remainders but number 2 did have a remainder of 2.
The quotient of question 2 can also be written as 712/3.
Question 3 had no remainder but the quotient can be simplified to 2x2+5x+3=(x+1)(2x+3).
Question 4 has a remainder like question number 2. it can be written as x3-4x2+2x-1=x2-2x-2-5/x-2
Instead of doing division the long way, we learned how to do synthetic division. This is what synthetic division looks like:

On Tuesday we started off the class by finding intercepts.
Find all intercepts
f(x)=4x3-7x+3
*The degree of the polynomial determines the maximum roots that the graph will have. Something like 4x4 could have up to 4 roots.
The first thing you do is find all the possible numerators (you can do this by finding all the factors of the constant in the equation):
±1, ±3
The next thing you do is find all the possible denominators (you can do this by finding all of the factors of the leading coefficient):
±1,±2,±4
From that you can find all the possible roots:
±/1, ±3/1, ±1/2, ±3/2, ±1/4, ±3/4
The easiest way to test if these are roots is by synthetic division:

If there is no remainder, which in this case there isn't, you take the linear factor (x-1) and add the x2 and the x where they belong then multiply the 2 to get the equation of the line.
f(x)=(x-1)(4x2+4x-3)
You can factor this further:
f(x)=(x-1)(4x2+4x-3)
f(x)=(x-1)[4x2+6x-2x-3]
f(x)=(x-1)[2x(2x+3)-1(2x+3)]
f(x)=(x-1)(2x+3)(2x-1)
From here you conclude that there are roots at (1,0), (1/2,0), (-3/2,0) and the y-intercept is at 3 because if you substitue 0 in for x in the equation, you are left with 3.
To draw the graph of this function, you must do a sign analysis. You must substitute numbers between the roots into the equation to check if they are negative or positive. The end result for this equation looks like this:

*The only way a root can change its sign is by passing through zero.
The graph of this function would look something like this:

On Wednesday we started by sketching the graph of f(x)=-2x3-7x22x+3.
These are the steps you take to graph this polynomial:
1.Factor everything
2.Find the y-intercept
3.Find the roots (You may use the roots theorem)
4.Do a sign analysis
5.Sketch the graph
This polynomial is easy to work with in this form.
The y-intercept is the constant which in this case is 3.
Find the roots by finding the possible roots and use synthetic division to find a root:

From this, you can also find points on the graph by using the possible root as the x-coordinate and the remainder as the y-coordinate. Here you have points at (1,-8), (3,-57), and a root at (-1,0)
You can factor the polynomial to find more roots by using the linear equation x+1 and multiplying it by the equation you got by using synthetic division:
f(x)=(x+1)(-2x2-x+3)
f(x)=(x+1)(-2x2-6x+x+3)
f(x)=(x+1)[-2x(x+3)+1(x+3)]
f(x)=(x+1)(x+3)(-2x+1)
From this you get roots at x=-3,-1,1/2 and you can sketch the graph of the polynomial. The graph would look something like this:

Now something like y=1/x would have a vertical asymptote on the y-axis and a horizontal asymptote on the horizontal axis. The graph would look like this:

The next scribe is eeDce
The steps to graphing a function like f(x)=1/x-2 would be:
1.Factor everything
2.Find the y-intercept
3.Find the roots
4.Find the vertical asymptote
5.Find the horizontal asymptote
6.Do a sign analysis
7.Sketch the graph
f(x)=1/x-2 is already factored
The y-intercept would be at y=-1/2
There would be no roots
The vertical asymptote would be at x=2
The horizontal asymptote would be found like this:
limx®¥ 1/x-2
limx®¥ (1/x)/(x/x-2/x)
limx®¥ (1/x)/(1-2/x)
=0/1-0
The horizontal asymptote would be at y=0 on the y-axis. An easier way to find the horizontal asymptote is by taking the leading coefficient of the denominatior and divide it by the leading coefficient of the numberator but only if they have the same degree.
The sign analysis would look like this:

The graph for this would look like this:

THE NEXT SCRIBE IS eeDce
January 22, 2007
January 21, 2007
Functions
Function: Functions are set(s) of rules that turn one mathematical object into another.

...the input changes to an output after adding one unit to it.
2) Graphically: Graph

3) Numerically: Table of Values

4) Symbolically: Equation
f(x) = x + 1

FUNCTIONS + RELATIONS
Four ways of presenting functions: [Using the function f(x) = x + 1]
1) VerbalFour ways of presenting functions: [Using the function f(x) = x + 1]
...the input changes to an output after adding one unit to it.
2) Graphically: Graph

3) Numerically: Table of Values

4) Symbolically: Equation
f(x) = x + 1
FLAVORS OF FUNCTIONS

in the above example; when the input is -2 the output is 3.5, and when the input is 2 the output is 3.5 again.
E.g f(x) = x - 3

for e.g.
 Note: We can use all the operations on function compositions.
Note: We can use all the operations on function compositions.
TEST FOR FUNCTIONS:
This is done by the vertical line test, which ensures that there's only one output for each input.
e.g. 1\ Passes 2\ Fails

1)Many-to-One Function
This is when a function provides one output for two or more inputs.
in the above example; when the input is -2 the output is 3.5, and when the input is 2 the output is 3.5 again.
2) One-to-One Function:
This is a kind function, where there's is only one output for one input.E.g f(x) = x - 3

FUNCTION COMPOSITION
Function composition dimply means: feeding a function into another.for e.g.
 Note: We can use all the operations on function compositions.
Note: We can use all the operations on function compositions.TEST FOR FUNCTIONS:
This is done by the vertical line test, which ensures that there's only one output for each input.
e.g. 1\ Passes 2\ Fails

Baby play + Parent clean up = Functions?
Hello!
Friday's class Mr.K wanted to tell us a story. He told us a story about his daughter playing in a play room, where she would disorganize everything. Then Mr.k and his wife would put everything back in place afterwards.
At first most of us thought it had nothing to do with functions.

This chart helped us understand more about inverse functions.
Inverse Functions: undoes the input of the function (Exchanging the domain and range)
We then moved on to some examples.
f (x) =2x-3 (inverse will be to divide. Changing the order of operations)
y=2x-3
Inverse functions of y=2x-3.
x=2y-3
x+3=2y
x+3/2=y or 1/2x + 3/2=y
We can really understand it more when we look at the table of values.
 Another example:
Another example:
f-1(x) = 3√5x2-2/6
x = 3√5y2-2/6
x3 = 5y2-2/6
6x3 = 5y2-2
6x3+2 = 5y2
6x3+2 = 5y2
6x3+2/5 = y2
√6x3+2/5 = y

The next scribe for tomorrow is Crysta!
Friday's class Mr.K wanted to tell us a story. He told us a story about his daughter playing in a play room, where she would disorganize everything. Then Mr.k and his wife would put everything back in place afterwards.
At first most of us thought it had nothing to do with functions.

This chart helped us understand more about inverse functions.
Inverse Functions: undoes the input of the function (Exchanging the domain and range)
We then moved on to some examples.
f (x) =2x-3 (inverse will be to divide. Changing the order of operations)
y=2x-3
Inverse functions of y=2x-3.
x=2y-3
x+3=2y
x+3/2=y or 1/2x + 3/2=y
We can really understand it more when we look at the table of values.
 Another example:
Another example: f-1(x) = 3√5x2-2/6
x = 3√5y2-2/6
x3 = 5y2-2/6
6x3 = 5y2-2
6x3+2 = 5y2
6x3+2 = 5y2
6x3+2/5 = y2
√6x3+2/5 = y

The next scribe for tomorrow is Crysta!
January 17, 2007
BOB - Logics
I'd have to say that this unit was quite different from the units that we previously worked on. Some parts were easier for me, so I hope I'll be able to boost up my mark through this. The same goes with everyone else. To be honest, I found it confusing at first, but since it related to real life, I began seeing the concept in a different perspective where I can understand it better. It definitely got my mind going though. So, hopefully this test will be smooth sailing for everyone.
Good luck everyone!
Good luck everyone!
Hey BoB .. you've got anything to say?...no? ...y?
Hey guys,
i couldn't get to class today. well, i had a doc. appointment, and then felt like i needed rest. so, anyhow...this unit i would say was pretty interesting and sometimes mentally challenging (well, not quite).
Logic + Statistics are my favourite branches of math, cuz they dont just relate to real life. They are real life lol. And in this unit, i would say i tried my best, and it went fairly good, accept that i missed the last day. anyways, I'm hopin that i didnt miss that much, and am looking forward for a good grade on this test.
Hope this test will boost up everyones average!
Nati
i couldn't get to class today. well, i had a doc. appointment, and then felt like i needed rest. so, anyhow...this unit i would say was pretty interesting and sometimes mentally challenging (well, not quite).
Logic + Statistics are my favourite branches of math, cuz they dont just relate to real life. They are real life lol. And in this unit, i would say i tried my best, and it went fairly good, accept that i missed the last day. anyways, I'm hopin that i didnt miss that much, and am looking forward for a good grade on this test.
Hope this test will boost up everyones average!
Nati
January 16, 2007
BOB TIMEE - LOGIC
My view on our logic unit was a fair stretch of our mind. I think we may have all found it difficult only because our state of mind and way of thinking differs from dealing with triangles and square roots. Some particular parts of this unit was very plain and simple (i.e: the venn diagrams). Others required more thought and time (i.e: deductive/inductive reasoning). Although everything was possible to solve with either a formula or a broad set of rules to be followed. I hope we all do well on this test. I know its getting harder to stay consitent with our motivation to do well because the course is so close to over. I know for myself, I find myself slacking because I'm just so ready to be done. I know it's not smart on my behalf and I can already see the consequences by suffering of overload before exams. I just need to straighten out and prepare myself with a logical matter! Okay. GOOD LUCK GUYS
I had a fun time BOBing. Hey guys its our last one!
I had a fun time BOBing. Hey guys its our last one!
Blogging on blobbing
I personally think that this logic unit was somekind of a very...very ... long stretch for my mind. I think that i struggle for the most part of this unit. Perhaps , the easiest thing in this unit was the venn diagrams and valid and invalid arguments. I think that I really have to study very hard tonight or else i'm done. Well thats it I hope that I didnt miss too much information from todays class. Study hard and keep your body away from sickness!! Good night
Direct and Indirect reasoning
Good evening everyonethis is m@rk scribing for yesterday's class. I've been banged up by high fever that is why i was unable to go to class today.
To start yesterday's class we proved using direct reasoning that the product of 2 even numbers is even too.First of all an even number is something that is divisible by 2 and has a factor of 2.
Let 2x=an even number
2a=another even number
2x * 2a =4ax
2x * 2a= 2 (2ax)
∴ Any product by both even numbers is also even as seen from above.
Then, we proved using direct reasoning that the product of 2 odd numbers is odd too.
Let (2x+1) =an odd number
(2a+1) = another odd number
(2x+1) (2a+1) =4ax+2x+2a+1
(2x+1) (2a+1)=2 (2ax+x+a) 1
∴ Any product by both odd numbers is also odd as seen from above because the product does not factor perfectly with 2.
Now, from the previous class we proved that √2 is irrational using indirect reasoning.
First, assume that √2 is rational.
√2=a/b
Note: a/b is in reduced form meaning they have no common factors.
2= a²/b² Multiply both sides by b²
2b² =a²
a² must be an even number and a must be even too so, let a=2c.
2b² = (2c)²
2b²=4c²
b²=2c²
b² and b are both even numbers so, let b=2d. This is a contradiction! Both a and b cannot have any common factors because of our assumption that they are in reduced forms in the beginning.
∴ √2 is irrational
Then, we prooved that √3 is irrational using indirect reasoning.
First, assume that √3 is rational. THis problem is similar to the the previous one.
√3= a/b
Assume that a/b is in reduced form.
3= a²/b²
3b² = a²
On the other hand lets look at square numbers first.
4= 2*2
9=3*3
16=2*2*2*2
25=5*5
36=2*3*2*3
49=7*7
64=2*2*2*2*2*2
81=3*3*3*3
100=5*2*5*2
Can you see the pattern that there is always a pair of prime numbers in square numbers?
So let b²=3c
3(3c)² =a ²
3* 9c² =a²
BUt it cannot happen because a and b will share the same factor which is 3. Therefore contradicting with our first statement that a and b is in reduced form.
∴√3 is irrational
Lastly, we talked about pardoxes. A paradox is a statement that cannot be true but also cannot be false.
Example:
This sentence is false
In this case you cannot decide whether it is true or false.
Thats it for my scribe for tonight. I dont know if im going to be able to go to class tomorrow. It all depends if im feeling better . LIke i told Mr. K the scribe will be Natnael. The homework is the Unusual school play
To start yesterday's class we proved using direct reasoning that the product of 2 even numbers is even too.First of all an even number is something that is divisible by 2 and has a factor of 2.
Let 2x=an even number
2a=another even number
2x * 2a =4ax
2x * 2a= 2 (2ax)
∴ Any product by both even numbers is also even as seen from above.
Then, we proved using direct reasoning that the product of 2 odd numbers is odd too.
Let (2x+1) =an odd number
(2a+1) = another odd number
(2x+1) (2a+1) =4ax+2x+2a+1
(2x+1) (2a+1)=2 (2ax+x+a) 1
∴ Any product by both odd numbers is also odd as seen from above because the product does not factor perfectly with 2.
Now, from the previous class we proved that √2 is irrational using indirect reasoning.
First, assume that √2 is rational.
√2=a/b
Note: a/b is in reduced form meaning they have no common factors.
2= a²/b² Multiply both sides by b²
2b² =a²
a² must be an even number and a must be even too so, let a=2c.
2b² = (2c)²
2b²=4c²
b²=2c²
b² and b are both even numbers so, let b=2d. This is a contradiction! Both a and b cannot have any common factors because of our assumption that they are in reduced forms in the beginning.
∴ √2 is irrational
Then, we prooved that √3 is irrational using indirect reasoning.
First, assume that √3 is rational. THis problem is similar to the the previous one.
√3= a/b
Assume that a/b is in reduced form.
3= a²/b²
3b² = a²
On the other hand lets look at square numbers first.
4= 2*2
9=3*3
16=2*2*2*2
25=5*5
36=2*3*2*3
49=7*7
64=2*2*2*2*2*2
81=3*3*3*3
100=5*2*5*2
Can you see the pattern that there is always a pair of prime numbers in square numbers?
So let b²=3c
3(3c)² =a ²
3* 9c² =a²
BUt it cannot happen because a and b will share the same factor which is 3. Therefore contradicting with our first statement that a and b is in reduced form.
∴√3 is irrational
Lastly, we talked about pardoxes. A paradox is a statement that cannot be true but also cannot be false.
Example:
This sentence is false
In this case you cannot decide whether it is true or false.
Thats it for my scribe for tonight. I dont know if im going to be able to go to class tomorrow. It all depends if im feeling better . LIke i told Mr. K the scribe will be Natnael. The homework is the Unusual school play
BOB
Another unit test coming up. For me, logic was a lot harder than I thought it would be. Even if it's not that easy, I personally enjoy the challenge of finding the solutions. I've had experience with these kinds of problems in junior high, so I have a good starting idea as to how to approach the question. I just hope that we all do really good on this test, and hopefully, I get the mark I've worked to get. 'Night!
BOB
This logic unit was interesting. It was cool getting back to the Venn-diagrams, bringing back the memories of arithmetic's in elementary. The good old days, everything was so simple. This unit got more difficult when we started the inductive and deductive reasoning. I'm still having trouble with that.
That's all, good luck to everyone tomorrow!
That's all, good luck to everyone tomorrow!
BOB v.6 The LOGICal Bob
Well I can't say the logic unit was straight forward since we now know about the paradoxes. It was fun though doing those paradox assignments on "A Usual Day at an Unusual School." Venn Diagrams were easy to do and so were the matrix problems. It felt like doing jr.high stuff but more advance. It was awesome learning logic in math class where we discuss things that barely have to do with numbers as compared to the other unit we're doing - consumer math. We discussed confusing things suchas "the inverse is the converse of the contrapositive" and the existence of counterexamples. Learning logic was fun and very interesting and the countdown begins for the logic test to show.
-Zeph
-Zeph
January 15, 2007
BOBing
This unit was alright, logic. It was difficult at first because I wasn't sure how to start solving the problems. I like doing problems where you figure out if it's a deductive information or inductive information. I also like doing problems where you verify if it's a valid argument or invalid argument.
What I found most difficult is when I try to figure out if the problem is a paradox or not. Proving that the square root of some numbers are irrational is also something that I find difficult as well. The consumer math stuff was alright. There were times where I didn't understand it, that was when the question asked about stuff I didn't know yet. My parents helped me, because they deal with this stuff all year round. Overall, consumer math was good and logic was quite difficult. Well, I'll see you all in class tomorrow fellow classmates and I hope you all study hard!
-SAMUS :D
What I found most difficult is when I try to figure out if the problem is a paradox or not. Proving that the square root of some numbers are irrational is also something that I find difficult as well. The consumer math stuff was alright. There were times where I didn't understand it, that was when the question asked about stuff I didn't know yet. My parents helped me, because they deal with this stuff all year round. Overall, consumer math was good and logic was quite difficult. Well, I'll see you all in class tomorrow fellow classmates and I hope you all study hard!
-SAMUS :D
BOB for Logics test in 1day and 16 hours
In logic we had done logical work like indirect and direct reasoning, inductive and deductive reasoning and that is what I am having trouble in. I don't understand the difference between the 2 reasoning in each set. I don't understand the definition on inductive and deductive reasoning.
Something that I am getting the hang of the is the Venn-diagram questions. They seem to be the easiest parts of logic.
In conclusion good luck everybody on the test that is happening in 1 day and 15 hours and 15 minutes from when I post this BOB :-)
Signed,
Benvolio (Ben)
Something that I am getting the hang of the is the Venn-diagram questions. They seem to be the easiest parts of logic.
In conclusion good luck everybody on the test that is happening in 1 day and 15 hours and 15 minutes from when I post this BOB :-)
Signed,
Benvolio (Ben)
blogging on blogging - logic
Well, this unit has gone by pretty fast. Of course that's not including the two weeks break we had. So not including that, it hasn't really been that many classes. Logic has been one of the more interesting, fun topics. Venn Diagrams, once you understand the method of how you put them together, they're pretty straight forward. And personally, if i know how to do something, it always makes it fun because i understand it. As for inductive and deductive, that's okay. i had some trouble at first, but nothing i couldn't fix. And what we did in class today was fun as well as our homework. So this unit isn't too bad.
Honestly, i can't remember if Mr. k said to do a blog for this unit or not? A lot of things lately have just been a dream, haha, so I'm not too sure. But better to do this than not to! Well, good luck everyone.
Honestly, i can't remember if Mr. k said to do a blog for this unit or not? A lot of things lately have just been a dream, haha, so I'm not too sure. But better to do this than not to! Well, good luck everyone.
Usual Day At Unusual School
We talked about proof by contradiction in the last couple of classes. Today we proved that √2 is irrational using proof by contradiction (which is also called, in latin, reductio ad absurdum). You can also review direct proof here (use the pop-up menu to review indirect proof and other topics as well).
Tonight's homework is the play below. Make a list of all the Braves and Brights. We'll discuss it in class tomorrow. ;-)
Page 1 of 4 Page 2 of 4 Page 3 of 4 Page 4 of 4
Tonight's homework is the play below. Make a list of all the Braves and Brights. We'll discuss it in class tomorrow. ;-)
Page 1 of 4 Page 2 of 4 Page 3 of 4 Page 4 of 4
January 13, 2007
Well like yesterday to start things off we had another quiz. The quiz was not on valid and invalid questions but learning how to draw venn-diagrams based on word problems. I thought the quiz was a little easier than yesterdays. Well after going over the quiz we got off topic and had an interesting discussion about this new device called a smart board. Well the smart board is a school board and a computer in one. It's basically an interactive white board. It's sound really cool and I hope Mr.K gets it in time for us to use it next semester.
Besides chatting about this cool smart board we actually did do some work. We learned about Direct and Indirect prove.
Direct Prove would be Thales' Theorem. We know if an inscribed angle in a circle is subtended by a diameter, then the angle is 90 degrees. Also that 2x+2y=180 degrees or that simplified x+y=90 degrees, as shown below.

Indirect prove is where you begin assuming the opposite of what we want to prove.
So here was the example that we worked on in class
Given triangle ABC with point D on line BC
Prove: If Line AB = AC
and angle BAD doesn't equal angle CAD
then line BD doesn't equal line CD
(so we start we assuming the opposite
line BD = line CD) "a contradiction"


That was the only example that we got to but the next scribe will be able to scribe on the good stuff as Mr. K described the ones we didn't get to yet.
Well the next scribe is m@rk so have fun ...........
Remember our go for golds due Wednesday before exams
and one of our two consumer worksheets on Monday
Besides chatting about this cool smart board we actually did do some work. We learned about Direct and Indirect prove.
Direct Prove would be Thales' Theorem. We know if an inscribed angle in a circle is subtended by a diameter, then the angle is 90 degrees. Also that 2x+2y=180 degrees or that simplified x+y=90 degrees, as shown below.

Indirect prove is where you begin assuming the opposite of what we want to prove.
So here was the example that we worked on in class
Given triangle ABC with point D on line BC
Prove: If Line AB = AC
and angle BAD doesn't equal angle CAD
then line BD doesn't equal line CD
(so we start we assuming the opposite
line BD = line CD) "a contradiction"


That was the only example that we got to but the next scribe will be able to scribe on the good stuff as Mr. K described the ones we didn't get to yet.
Well the next scribe is m@rk so have fun ...........
Remember our go for golds due Wednesday before exams
and one of our two consumer worksheets on Monday
January 11, 2007
Hey guys exams are coming.
Well to start things off we had quiz. The quiz was of course on logic, inductive, deductive, valid and invalid questions. A inductive statement is where you have examples and make a generalization and deductive statement is where you have a generalization and produce an example. The part I thought some of us had problems with was determining whether a statement was valid and invalid. Anyways tomorrow might be the logic test so remember to have your BOB's up just in case. Besides the quiz we had a lot of writing to do in our math dictionaries some new and old things.
Well to start things off we had quiz. The quiz was of course on logic, inductive, deductive, valid and invalid questions. A inductive statement is where you have examples and make a generalization and deductive statement is where you have a generalization and produce an example. The part I thought some of us had problems with was determining whether a statement was valid and invalid. Anyways tomorrow might be the logic test so remember to have your BOB's up just in case. Besides the quiz we had a lot of writing to do in our math dictionaries some new and old things.
MATH DICTIONARY
Some definitions
Set: A collection of objects (could be people, things, numbers etc.)
Subset: A collection of objects that consists of some, all or none of the objects in a given set
Example: Consider set A :(1,2,3)
All of the following are subsets of A : (1), (2), (3), (1,2), (1,3), (2,3), (1,2,3),
Note: is called the "empty set" or "null set" but is still a subset of every set
is called the "empty set" or "null set" but is still a subset of every set
Universe (U) : all objects are being considered
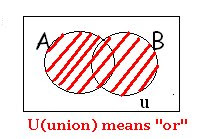
Notation: Union U A U B means gather all objects in set A with all objects in set B

Notation: Intersection
Intersection
 means gather all the objects that are both in set A and B
means gather all the objects that are both in set A and B

- or ' compliment: (reads as " the compliment of A" or "A compliment") means everything outside A
(reads as " the compliment of A" or "A compliment") means everything outside A

 exclusion:
exclusion:  means everything that is in set A but not set B
means everything that is in set A but not set B

Counterexample: Given any logical argument, theorem or hypothesis, if you can find only one case where it is not true, then the theorem or argument is proven false . This is called a "counterexamlple"
Conditional statements: Any statement of the form" If...then..." is called a "conditional" or "implication"
Hypothesis: The first part of the conditional
Conclusion: The second part of a conditional
Example: If(hypothesis) Then(conclusion)
If a triangle is isosceles Then it's base angles are congruent
Well that's all for this scribe and I'll scribe on Friday since I couldn't get my post up in time.
Homework is Ex. 48
Flickr assignment due this Friday
Go for Gold due Wednesday before exam
and our 2nd consumer packet

Set: A collection of objects (could be people, things, numbers etc.)
Subset: A collection of objects that consists of some, all or none of the objects in a given set
Example: Consider set A :(1,2,3)
All of the following are subsets of A : (1), (2), (3), (1,2), (1,3), (2,3), (1,2,3),

Note:
 is called the "empty set" or "null set" but is still a subset of every set
is called the "empty set" or "null set" but is still a subset of every setUniverse (U) : all objects are being considered
Notation: Union U A U B means gather all objects in set A with all objects in set B


Notation:
 Intersection
Intersection means gather all the objects that are both in set A and B
means gather all the objects that are both in set A and B
- or ' compliment:
 (reads as " the compliment of A" or "A compliment") means everything outside A
(reads as " the compliment of A" or "A compliment") means everything outside A
 exclusion:
exclusion:  means everything that is in set A but not set B
means everything that is in set A but not set B
Counterexample: Given any logical argument, theorem or hypothesis, if you can find only one case where it is not true, then the theorem or argument is proven false . This is called a "counterexamlple"
Conditional statements: Any statement of the form" If...then..." is called a "conditional" or "implication"
Hypothesis: The first part of the conditional
Conclusion: The second part of a conditional
Example: If(hypothesis) Then(conclusion)
If a triangle is isosceles Then it's base angles are congruent
Arguments of the form"if..then..." and related statements
A sentence that says only one thing is called a "declarative sentence"
Well that's all for this scribe and I'll scribe on Friday since I couldn't get my post up in time.
Homework is Ex. 48
Flickr assignment due this Friday
Go for Gold due Wednesday before exam
and our 2nd consumer packet

January 10, 2007
LOGIC
Salutations fellow classmates,
Rules for Go For Gold:
1) only two options for marks; zero or one hundred.
2) you may talk to other students.
3) you can ask Mr. K ONLY one question.
4) you must complete it and hand it in on time. (it IS a good way to prepare for the exam)
Today in class, for all you naughty kids that skipped (haha jk), we kind of had a work period. Mr. Kurropatwa had to leave for some meeting, but before that, he had handed out the Go For Gold assignment, which is to be due in about 2 weeks from now.
Rules for Go For Gold:
1) only two options for marks; zero or one hundred.
2) you may talk to other students.
3) you can ask Mr. K ONLY one question.
4) you must complete it and hand it in on time. (it IS a good way to prepare for the exam)
He also handed out the second consumer math booklets. We only got one worksheet to fill in for now and the other worksheets will be handed to us tomorrow. Tomorrow's not a good day to skip then ;)
He also told us that our other project is up and running, the wiki. There will be enough questions for at least everyone to do. Here's the link to it: www.pc20sf06.pbwiki.com
Our photo trigonometry projects are due today and we received our rubric on how we're being marked.
Our photo trigonometry projects are due today and we received our rubric on how we're being marked.
Throughout the class, we all worked on our Go For Gold. Hopefully everyone does well on that, and we all get 1 hundred! Remember to work on the wiki and to go to class tomorrow because we get our worksheets (and who doesn't like to get an early start on work? lol). Yeah, and that's about it. Our next scribe for tomorrow will be
...............................................................................
...............................................................................
...............................................................................
...............................................................................
...............................................................................
...............................................................................
...............................................................................
...............................................................................
...............................................................................
LAURESSA!!! :D
January 08, 2007
Peter Donnelly
Oxford statistician Peter Donnelly explores the common mistakes humans make in interpreting statistics, and the devastating impact these errors can have on the outcome of criminal trials.
You will learn the math he's talking about here in your grade 12 Pre-=Cal class ... probability.
Click on the picture. (22 min. 6 sec.)

You will learn the math he's talking about here in your grade 12 Pre-=Cal class ... probability.
Click on the picture. (22 min. 6 sec.)

New Year With Continuation of Last Year's Class
Hi and happy new year everybody and I hope you all had a great holiday. Today we continued on what we left off on the last day of school before the holidays. We worked on some word problems that had to do with Venn- Diagrams. These are the questions:
1. Recently several DMCI students were surveyed about their favourite music groups.
The results were:
b) How many students liked U2 only?
c) How many students like exactly 2 groups
2.Every year over 9 million tourists visit Turkey. Last year 9.8 million tourists vistited Turkey.
Solutions
1.So first we fill in a three circle venn diagram because there are 3 different groups.
I'll explain the diagram, first we work our way from the middle and we know that there are 6 people who like all three groups. Now we pick one of the next 3 overlaps and find those. Lets use U2 & Hole as an example, we know from the clues that 9 people liked Hole & U2 so we subtract 6 from the 9 because the 6 represents 6 people that also like Hole & U2. So we have 3 in that section. Once those sections are complete we work on the outer sections. Like the overlaps we take the total number of people that like that group and subtract the number of people that like that group and other groups also.
a)This question asks us to find the number of students survey, so we just add all the numbers up and we get 50
b)This question asks us to find the number of students who only liked U2 and the answer is 2 according to the graph
c)This question asks us to find the number of students who like only 2 groups and the answer is 28. We get that by adding the numbers that are in the section of 1 overlap which are 3, 11, 14.
2.This quest is a doozy because we have to go back and forth with the clues.
1. Recently several DMCI students were surveyed about their favourite music groups.
The results were:
- 22 like Hole
- 25 like U2
- 39 like Third Eye Blind (TEB)
- 9 like U2 & Hole
- 17 like Hole & TEB
- 20 like U2 & TEB
- 6 like all three
- 4 like non of these three
b) How many students liked U2 only?
c) How many students like exactly 2 groups
2.Every year over 9 million tourists visit Turkey. Last year 9.8 million tourists vistited Turkey.
- 60% visited only Istanbul
- 20% visited Izmir
- Half of the tourists who visited Izmir also visited Istanbul
- 2% visited Istanbul, Izmir, and Antalya
- The number of tourists who visited only Antalya was half again as much as the number of the tourists who only visited Izmir
- Tourists who visited Antalya either saw only Antalya or Antalya, Istanbul, and Izmir
- The rest of the tourists visited other regions
Solutions
1.So first we fill in a three circle venn diagram because there are 3 different groups.

I'll explain the diagram, first we work our way from the middle and we know that there are 6 people who like all three groups. Now we pick one of the next 3 overlaps and find those. Lets use U2 & Hole as an example, we know from the clues that 9 people liked Hole & U2 so we subtract 6 from the 9 because the 6 represents 6 people that also like Hole & U2. So we have 3 in that section. Once those sections are complete we work on the outer sections. Like the overlaps we take the total number of people that like that group and subtract the number of people that like that group and other groups also.
a)This question asks us to find the number of students survey, so we just add all the numbers up and we get 50
b)This question asks us to find the number of students who only liked U2 and the answer is 2 according to the graph
c)This question asks us to find the number of students who like only 2 groups and the answer is 28. We get that by adding the numbers that are in the section of 1 overlap which are 3, 11, 14.
2.This quest is a doozy because we have to go back and forth with the clues.
If the pictures are going too fast, feel free to pause or replay.
After the explanation of those two questions we began with a new logic subject.
Mr. K told us to take out a new piece of loose leaf and draw the biggest circle you can draw on that paper and make a dot on the circumference. Then he asked us how many different flat areas there are in the circle and there are 1. He told us to make a second dot and connect the dots and asked us how many areas are there and there were 2. Then a 3rd dot and then connect that dot with every other dot and then do the same as before and there were 4 areas. Now look at the graph.
at the graph.
This album is powered byBubbleShare
- Add to my blog
So lets think of an equation to helps us find the number of areas if the number of points is 457.
As a class we discovered that the equation 2(n-1) where n is the number points will work. So we tried the equation with 6 as the number of points and using the equation we predicted the number of areas will be 32. Now continue with the diagram with 6 dots and count the number of areas. Oh no there is only 31. That is situation called a counterexamples and that is when there is a theorem made and there is one example that doesn't fit the theorem. That just makes the theorem a theorem that is not true. Tomorrow will be the continuation about counterexamples.
Okay that was our first class back from the holidays and it was kind of tiring to go back to school after a 2 week break. Homework (homework*sigh*) is exercise #48 and it is about counterexamples.
The next scribe will be SAMUS!!!
Good Night :-)
- The first picture shows inserting the info from the first clue and from the clue it tells us that 60% of the total tourists visited only Istanbul. We can put it on the venn diagram because the clue states that 60% visited only Istanbul.
- The second picture shows the third clue and with the second clue in mind we can find the Istanbul- Izmir overlap because the clue states that half of the number of tourists that visited Izmir also visited Istanbul. So half of 20% is 10% and that leaves us with 10% for Izmir.
- The third picture shows the addition of the middle section with the forth clue.
- The forth picture shows the sixth clue which states that the people who visited Antalya only visited Antalya or saw all three places and not 2 places. So we know that the Izmir-Antalya and Istanbul-Antalya sections have 0%'s. And now we can find how many people visited Izmir and it is 8% because before we had 10% and due to the forth cluwe are left with 8% and that 8% go into the Izmir section.
- The fifth picture shows the fifth clue and it states that the people that visited Antalya is equal to 1.5x the number of people who visited Izmir and 8 x 1.5= 12. So Antalya is 12%.
- The final picture shows the addition of the last clue which states that the remainder of the tourists visited other regions.
After the explanation of those two questions we began with a new logic subject.
Mr. K told us to take out a new piece of loose leaf and draw the biggest circle you can draw on that paper and make a dot on the circumference. Then he asked us how many different flat areas there are in the circle and there are 1. He told us to make a second dot and connect the dots and asked us how many areas are there and there were 2. Then a 3rd dot and then connect that dot with every other dot and then do the same as before and there were 4 areas. Now look
 at the graph.
at the graph.This album is powered byBubbleShare
- Add to my blog
So lets think of an equation to helps us find the number of areas if the number of points is 457.
As a class we discovered that the equation 2(n-1) where n is the number points will work. So we tried the equation with 6 as the number of points and using the equation we predicted the number of areas will be 32. Now continue with the diagram with 6 dots and count the number of areas. Oh no there is only 31. That is situation called a counterexamples and that is when there is a theorem made and there is one example that doesn't fit the theorem. That just makes the theorem a theorem that is not true. Tomorrow will be the continuation about counterexamples.
Okay that was our first class back from the holidays and it was kind of tiring to go back to school after a 2 week break. Homework (homework*sigh*) is exercise #48 and it is about counterexamples.
The next scribe will be SAMUS!!!
Good Night :-)
January 07, 2007
VEry ...very late post
Ok, everyone I hoped you had some very good days of rest. Now, let's start with the math. I know that this should have been posted a long time ago but my computer sort of meltdown.First of all I need to thank my cousins for fixing my computer and making me recovery disks.
Last two weeks we reviewed the questions from our circle unit. The first question was:
Given:
line AP and line AQ are tangents
Arcs BS and RE are congruent
Angles 2 and 5 are congruent
Prove that lines BC and ED are congruent
 Statement and Reason
Statement and Reason
Lines AB and AE are congruent Tangent Theorem
Angles 3 and 4 are congruent Inscribed Angle Theorem
Triangles ABC and AED are congruent Angle-angle-side
LInes BC and ED are congruent From above
The second question was:
Isosceles triangle ABC is inscribed in a circle with a diameter 12 cm. Side AB is a diameter. Determine the length of BC.
 Let X=the length of lines AC and BC.
Let X=the length of lines AC and BC.
Then use the phythagorean theorem
x^2+x^2=12^2 2x^2=144
x^2=72
x=√72
x=6√2
The third question was:
Quadrilateral PQRS is inscribed in a circle. Side PQ is parallel to side SR. The diagonals intersect at T. Prove that triangles TSR and TPQ are isosceles.
 Statement and Reason
Statement and Reason
Arcs PS and QR are congruent Parallel Chords Theorem
Lines PT and QT are congruent Congruent chords theorem
Lines ST and RT are congruent Congruent chords theorem
TRiangles TSR and TPQ are isosceles From above
The fourth one was:
The circle with centre O has 4 points of tangencyA,B,C and D.Angle AEB =30°, angle ADC=90, and Angle DCB=85.FInd the measure of angle CDG. Statement And Reason
Statement And Reason
Angle BAD=95 Cyclic Quadrilateral Theorem
LInes EA and EB are congruent Tangent theorem
Triangle AEB is isosceles From above
Angles EAB and EBA=75 BAse Angles
LInes HD and HA are congruent Tangent theorem
Angle HAD =10 Supplementary angles
Angle HDA=10 base angles
Angle CDG=80 Supplementary angle
Then after we reviewed the test we practiced on more stuff on Logic
The first question was: A survey of 80 students showed that 45 like rock music, 25 liked country and 10 liked both. How many liked neither?
 The second question was:
The second question was:
140 homes are surveyed 90 have a stereo, 70 have a DVD player and 40 have both. HOw many have neither?
 The last question was:
The last question was:
150 people were surveyed on their reading preferences
90- mystery
70- history novels
45-sci-fi
30-mystery and history
25- mystery and sci-fi
22-history and scifi
10 -reads all 3
How many read
1. At least one type of book
2. Exactly one type
3 Exactly two types
4. Do not read any of the 3 types
 That's it for this edition of my scribe. Again, i'm sorry for the images because my paint and RFXsoftware is not working properly eversince last year. I must admit that i need a new computer.
That's it for this edition of my scribe. Again, i'm sorry for the images because my paint and RFXsoftware is not working properly eversince last year. I must admit that i need a new computer.
REMINDERS
Flicker Assignment (trigonometry)
DElicious (Put at least one link for every unit we finished)
Last two weeks we reviewed the questions from our circle unit. The first question was:
Given:
line AP and line AQ are tangents
Arcs BS and RE are congruent
Angles 2 and 5 are congruent
Prove that lines BC and ED are congruent
 Statement and Reason
Statement and ReasonLines AB and AE are congruent Tangent Theorem
Angles 3 and 4 are congruent Inscribed Angle Theorem
Triangles ABC and AED are congruent Angle-angle-side
LInes BC and ED are congruent From above
The second question was:
Isosceles triangle ABC is inscribed in a circle with a diameter 12 cm. Side AB is a diameter. Determine the length of BC.
 Let X=the length of lines AC and BC.
Let X=the length of lines AC and BC.Then use the phythagorean theorem
x^2+x^2=12^2 2x^2=144
x^2=72
x=√72
x=6√2
The third question was:
Quadrilateral PQRS is inscribed in a circle. Side PQ is parallel to side SR. The diagonals intersect at T. Prove that triangles TSR and TPQ are isosceles.
 Statement and Reason
Statement and ReasonArcs PS and QR are congruent Parallel Chords Theorem
Lines PT and QT are congruent Congruent chords theorem
Lines ST and RT are congruent Congruent chords theorem
TRiangles TSR and TPQ are isosceles From above
The fourth one was:
The circle with centre O has 4 points of tangencyA,B,C and D.Angle AEB =30°, angle ADC=90, and Angle DCB=85.FInd the measure of angle CDG.
 Statement And Reason
Statement And ReasonAngle BAD=95 Cyclic Quadrilateral Theorem
LInes EA and EB are congruent Tangent theorem
Triangle AEB is isosceles From above
Angles EAB and EBA=75 BAse Angles
LInes HD and HA are congruent Tangent theorem
Angle HAD =10 Supplementary angles
Angle HDA=10 base angles
Angle CDG=80 Supplementary angle
Then after we reviewed the test we practiced on more stuff on Logic
The first question was: A survey of 80 students showed that 45 like rock music, 25 liked country and 10 liked both. How many liked neither?
 The second question was:
The second question was:140 homes are surveyed 90 have a stereo, 70 have a DVD player and 40 have both. HOw many have neither?
 The last question was:
The last question was:150 people were surveyed on their reading preferences
90- mystery
70- history novels
45-sci-fi
30-mystery and history
25- mystery and sci-fi
22-history and scifi
10 -reads all 3
How many read
1. At least one type of book
2. Exactly one type
3 Exactly two types
4. Do not read any of the 3 types
 That's it for this edition of my scribe. Again, i'm sorry for the images because my paint and RFXsoftware is not working properly eversince last year. I must admit that i need a new computer.
That's it for this edition of my scribe. Again, i'm sorry for the images because my paint and RFXsoftware is not working properly eversince last year. I must admit that i need a new computer.REMINDERS
Flicker Assignment (trigonometry)
DElicious (Put at least one link for every unit we finished)
Subscribe to:
Comments (Atom)






