Analytic Geometry

Hello everyone!.
Today in class Mr. K said we were going to learn something new and other stuff we already knew about.

We worked on two questions:

1) If the distance from the line 2x-3y+8=0 to the line 2x-3y+K=0 is 24/√13 units find the value(s) of K.

2) Given:A (-1,3)
B (0,5)
C (-2,6)

a) Is ABC a right triangle?
b) Is ABC isosceles?
c) If M is the midpoint of AB and N is the midpoint of AC prove that MN // BC
d) Find a point D so that ABCD is a parallelogram
e) is ABCD a rectangle?

We were given some time to work on it. Most of the class had trouble with the first question like where to start.

* For the first question we talked about ways to find out if the lines were parallel ( // ).We knew that if the slopes were the same they are //.

some examples shown.

a) 2x-3y+8=0
4x-6y-k=0
* multiplied by 2

b) 2x-3y+8=0
-8x-12y+k=0
* multiplied by -4

-back to solving question #1

1) We changed the first line to be written in Standard Form

2x-3y+8=0 | 3y=2x+8
y=2/3x+8/3

From changing it to standard form we found the y intercept and the x intercept.

y intercept (0, 8/3)
x intercept (-4,0)

We looked at the question again and wrote down all the information we knew.

P (-4,0)
A= 2
B=-3
C=K
D=24/√13

Now that we know all of this information we just replaced them in the formula to find a distance from a point to a line.
D = | Ax + By + C | / √A2 + B2

24/√13 = | 29(-4) -3 (0) +K | / √4+9

24/√13 = | -8+k | / √13

24 = | -8+K |

24= -8+K -24 = -8+K

32= K -16 = K

The answer to this question has 2 Values, which are 32 and -16.


The second question wasn't all answered, but this is what i got.




2)

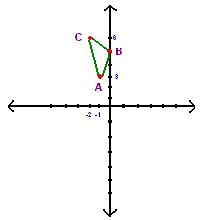
D = √(x2 -x1)2 + (y2-y1)2

AB=√1+4
=√5

BC =√4+1
=√5

CA =√9+1
=√10

(√5)2 + (√5)2 =√10

a) ABC is a right triangle
b) ABC is not a isosceles


* If anyone has more answers to this question feel free to comment and I'll update it. =)

Today we also wrote in our dictionaries, most of the information we already know.

My Analytic Geometry Tool Kit

The Pythagorean theorem | a2 + b2=c2

Slope of a line (a.k.a. rate of change) | (tri)y/(tri)x = y2 -y1/x1- x2

Midpoint of a line segment | midpoint = (x1-x2/2 , y1+y2/2)

Distance between two lines | D = √(x2 -x1)2 + (y2-y1)2

Distance between a point and a line | D = | Ax + By + C | / √A2 + B2

Equation of a lines

General Form | Ax+By+C=0

Standard Form | y=mx+b

Point-slope form | y2-y1=m(x2-x1)

Parallel lines (//) have equivalent slopes | m1-m2

Perpendicular lines have slopes which product is (-1) | m1-m2=-1

**Homework for today is exercise #23, and last the scribe for tomorrow is......-Zeph!!! Have fun!