Solving Inequalitie Equtions & A Splash of Review

Well well well. Another friday scibe post!
Okay. So lets get this scribe going.

Minutes after the 5th period bell, we all walk into our Pre-Cal class, as we do everyday and by our dismay we spot Mr. K holding a small stalk of papers. Since we're all "smarter then the average bear", we immediately knew a lovely quiz was coming in our direction. So after a brief discussion of wither or not we should include quizes for marks, we all got to work. The quiz was nothing new; a nicely summed up quiz about everything we learned so far in 'Analytic Geomtry'.

After self marking our peer's quizes, Mr. K placed the following questions on the board.

S O L V E:

Question 1:
x²+x<6

Okay, so we haven't seen much of these before and you may be a little puzzled.
BUT- think back to the Mathmatician who set the house on fire
"Turn the problem into something we already know how to solve"

First and foremost- Ignore the "<" for now, think of it as an "="
x²+x=6

And if we move the 6 to the opposite side..
x²+x-6=0

Why what do we have here? A parabola! Not too terrifying is it?

Okay so lets place the "<" back.
x²+x-6<0

Before actually solving this equation, it would help to understand what infact the question is asking. Well what we're trying to do is-
"Find the values of X where this parabola will have negative values"

So first we must factor the equation we came up with
x²+x-6<0
(x+3)(x-2)<0



Once we get the two roots, you must draw the line graph (it will be included for marks for the final answer). Finally pick any point in each of the 3 regions and sub it into the equation.

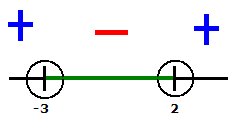
Answer: (-3, 2)
Remember! we use round brackets "( )" because we know the -3 and 2 are not included because the original equation did not include "≤" (less then AND equals to)



Question 2:
2x-3=5

Remember! The values in the absolute signs "x" can be both negative and positive, leaving us with two cases.

Case #1
2x-3=-5
2x=-2
x=-1 check: it works!

Case #2
2x-3=5
2x=8
x=4 check: it works!

Okay that was simple enough, BUT- what if we had..
2x-2>5

Yikes! Do not fear, remember- ignore the "<" and treat it as an "=" for now.

So we'd continue to solve just like before-
Case #1
2x-3>5
2x>8
x>4

Case #2
2x-3>-5
2x>-2
x>-1

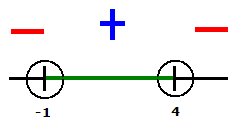
Answer: (-∞,1)U(4,∞)
"U" - Union, that group together with this group

To be finished soon, very soon.
Sorry folks!

Homework assignment: All the questions you didn't get done on the past exercises (up to Exercise 28).
Mondays scribe will be Mel!isa

.
.
Enjoy your weekend!