Quadratic Functions Review: Completing the square and Word problems

Hey everyone,

We started last Friday's class with a little discussion about our blog. Mr. K introduced us to the new features of our blog like the Blogging on blogging (BOB), shoutbox and links for learning. Then he continued with some questions we had trouble with from the Quadratic functions review.

The first one was: 2x^2-5x-8= 0
Completing the square:
2[x^2-5/2x+(5/4)^2-(5/4)^2] -8=0 Factor 2 out and then we have to multiply the middle term by 1/2 and square it to get the absolute values that completes the square. Simplify the term (5/4)^2
2[(x-5/4)^2-25/16]-8=0 Multiply the 2 in and change -8 into a fraction
2(x-5/4)^2-25/8-64/8=0 Add the like terms -25/8 and -64/8
2(x-5/4)^2-89/8=0

Finding the roots:
2(x-5/4)^2 =89/8 Add 89/8 to both sides
(x-5/4)^2=89/16 Multiply both sides to 2
x-5/4=+-sqrt of 89/16 Square root both sides
x=5/4+-sqrt of 89/4 Add 5/4 to both sides
x=5+-sqrtof 89/4 Combine like terms

The second one was: y=-3x^2-4x+7
Completing the square:
y=-3[x^2+4/3x+(2/3)^2-(2/3)^2]+7 Factor -3 out and then multiply the middle term by 1/2 and square it to get the absolute value that completes the square. Simplify the term(2/3)^2
y=-3[(x+2/3)^2-4/9]+7 Multiply the -3 in and change 7 into a fraction
y=-3(x+2/3)^2+12/9+63/9 Add like terms.
y=-3(x+2/3)^2+75/9

Finding the Roots:
y=-3x^2-7x+3x+7
y=-x(3x+7) +1 (3x+7)
y=(3x+7) (-x+1)


Now let's graph it :

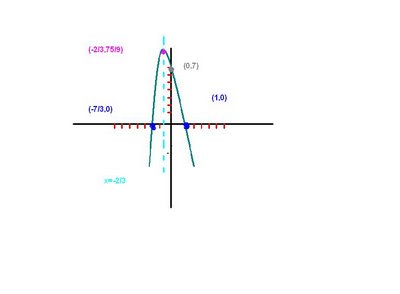
The third one was a little bit different from the question from the sheet. Instead of only using 2 widths we used four.

2L+4w=400 Divide the whole equation by 2
L+2W=200 Transpose 2w to the other side thus changing its sign. Now we got the length.
L=200-2W

Area= (length) (width) Now just sub-in the values
A(w)+(200-2w)w

Wv=100+0/2 Where did i get this values? Find the two values of w in the equation above to make it equal to zero. Then divide it by 2 to get the vertex.
Wv=50

The fourth one was:

The school theatre can seat 800 people. The cost of a ticket to the schoolplay is $3.00. At that price all the seats are sold. A survey indicates that if the price is increased, attendance will fall by 100 people for each dollar of increase. What ticket price will result in the greatest revenue? What is the greatest revenue? How many people will attend the play?

Revenue=(Cost/Ticket) (# of people)
Let x=1 increase in price of $1.00
R(x)= (3+x) (800-100x)
Xv=(-3+8)/2 Again, where did I get this values? Find the two values of x in the equation above to make it equal to zero. Then divide it by 2 to get the vertex.
Xv=2.5

R(2.5)= (3+2.5) (800- 100(2.5)) Just substitute 2.5 to x
R(2.5)= (5.5) (550) Now we've answered all the questions.
R(2.5)=$3025

Finally, the last question was:

On a forward somersault dive, Stacey's height ,h metres above the water is given by h=-5t^2+6t+3, where t is the time in seconds after she leave the diving board.

a. Find Stacey's maximum height above the water.
h(t)=-5t^2+6t+3
h(t)=-5[t^2-6/5t+(3/5)^2-(3/5)^2]+3 Factor the -5 out and then multiply the middle term by 1/2 and square it. Simplify (3/5)^2.
h(t)=-5[(t-3/5)^2-9/5]+3 Multiply -5 back in and change 3 to a fraction.
h(t)=-5(t-3/5)^2+9/5+15/5 Combine like fractions
h(t)=-5(t-3/5)^2+24/5 Therefore k=24/5 is the maximum height above water

b. How long does it take her to reach her maximum height?
At the equation above h=3/5, therefore it took her .6 of a second to get to 4.8 metres

c. How long is it before she enters the water?
0=-5(t-3/5)^2+24/5
5(t-3/5)^2=24/5
t-3/5=24/25
t=3/5+-sqrt of 24/5
t=3+-sqrt of24/5

d. How high is the diving board above the water?
On the original equation, h(t)=-5t^2+6t+3 the y-intercept is equal to 3 which means its her starting point.

That's it for my first scribe of the year. thnx everyone for spending 10 minutes of your time on reading my scribe. Our homework for the weekend STUDY!!!!! for our test and dont forget your BOB , because every mark counts...

Oppss... One more thing dont forget to do our Pretest sheet. the next scribe will be the last man standing Diyaa...