Review on Trigonometry

Hi every one. On today's (October 10, 06) class we did a pre-test, which was a review on what we've been working on, in this unit. These are the problems and their solutions.

Q1 Find the length of 'x' in the figure below.
Note: The 1o` in triangle ADC wasn't given. We found that because we subtracted 30` from 40`.
IS X = a) 22 b)31 c)30 or d)52

The easiest way is to find the length of BC and BD using the trig. ratios (SOHCAHTOA) and then subtract BD from BC.

BC
tan(40) = BC / 200
BC = tan(40)*200
BC = 167.8

BD or h
tan(30) = BD / 200
BD = tan(30)*200
BD = 115.5

Therefore SINCE X=BC - BD
X=167.8 - 115.5
X=52.3
OR (d)

Q2 How many triangles can be constucted with A=30`, a=4, and b=10?
Is it: a) none b) 1 c) 2 d) Can't be determined?

First off lets try to sketch the info given.

Using the sine law
Sin(30) / 4 = SinB / 10
SinB = Sin(30)*10 / 4
SinB = 0.5 * 10 / 4
SinB=1.25
ooooops!?! THE MAX VALUE FOR SINE OF AN ANGLE IS 1 (The # is too big!)

Q3 SOLVE 3CosA - 2 = 0 so that A is greater than 0` and less than 360`

3Cos(A) - 2 = 0
3Cos(A)=2
Cos(A)=2/3

A=Cos inverse (2/3)
A = 48`
But since Cos is positive in Quadrant 4 as well we have to get the other value that could possibly have a related angle of 48`
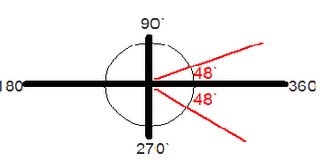Therefore the other angle =360`- 48`= 312`
The answer to the Q is: A = 48`, 312`

Q4 How would you calculate the reference of the angle J pictured below


Refrence or R
R = 180 - J
and you are done!

Q5 AHN OBSERVES THA ANGLE OF ELEVATION OF A PLANE TO BE 48`. AT THE SAME INSTANT, THE ANGLE OF ELEVATION FOR CRYSTAL IS 34`. AHN AND CRYSTAL ARE 80KM APART ON LEVEL GROUND.

A) How far is Ahn from the Plane?
B) How far is Crysta from the plane?
C) How high is the plane?

Step1 sketch the info given.

There are 2 ways that this triangle.

Whereby P=Plane A=Ahn C=Crytal

Note: That the numbers in blue weren't given, but we can get the numbers if we solve the triangle using the 180` principle.

A)
Sin(34`)/AP = Sin(98`)/80
AP = 80Sin(34`)/Sin(98`)
AP=45Km

Sin(14)/80 = Sin(34)/AP
AP = 80Sin(34)/Sin(14)
AP=237.9KM

B)
Sin(48`)/CP = Sin(98`)/80
CP=80Sin(48`)/Sin 98
CP=60KM

Sin(14`)/80 = Sin(132`)/CP
CP = 80Sin(132`) / Sin(14`)
CP=245.7KM

C)
Using trig. ratios
SinC = h/CP
Sin(34`) = h/60
h = 60Sin(34`)
h = 33.6KM

Using trig. ratios again
SinA = h/AP
Sin(48`) = h/237.9
h = 237.9Sin(48`)
h=176.8KM

I think I'm done.
.
.
The next scribe will be.
.
.
-Zeph