Trig Review: Trigonometrically Speaking Problem 1

LEGEND KEY

PURPLE - question/problem
GREEN - how to solve the problem
PINK - titles/captions...
ORANGE - flashbacks
TEAL - A/N (Author's Notes)
GOLD - answer in sentence form


so....kuropatwa started talking about computer programs and stuff and i wont go into detail on that 'cause i've found a much more easier way of doing things. based on kuropatwa's speculation on the BOB's, kuropatwa concludes that these two problems should give the students the most difficulty. we did two problems. i will label them "Problem #1" or "Problem #2."


FORMULA REVIEW


PYTHAGOREAN THEOREM

a^2 + b^2 = c^2

a and b are the legs of the triangle meaning that the values of a and b are interchangeable and c is the hypotenuse.

- recommended for right triangles


TRIGONOMETRIC RATIOS (SOH CAH TOA)

SOH meaning sin theta = opposite/hypotenuse
COH meaning cos theta = adjacent/hypotenuse
TOA meaning tan theta = opposite/adjacent

- recommended for right traingles


SINE LAW

- use sine law to find the side or angle of any triangle when an angle and its opposite side, and another angle OR side is given [recommended for oblique triangles (non-right triangles)]

(sin A / a) = (sin B / b) = (sin C / c) OR (a / sin A) = (b / sin B) = (c / sin C)

(a, b, and c are the sides of the triangle and A, B, and C are the angles)


COSINE LAW:

- use cosine law to find the side or angle of any triangle when SSS (side, side, side) or SAS (side, angle, side) are given. [recommended for oblique triangles]

a^2 = b^2 + c^2 - 2ab cos A

(a, b, and c, refers to the sides and A refers to the angle)

- this formula can be re-arranged to find the angle:

cos A = (b^2 + c^2 - a^2) / 2ac


yeah...so we will be using these forumlas in Problems 1 and 2.

just in case if you don't know...

angle of elevation - the angle that your line of sight that makes with the horizontal line when looking up

angle of depression - the angle that your line of sight that makes with the horizontal line when looking down


PROBLEM #1:

The pictcher's mound on a baseball diamond is 15.2 m from home plate. The distance between the bases is 19.8 m. How far is the pitcher's mound from the first base?

Step 1: Drawing the Diagram and Declaring Variables

first we draw a picture of the situation:





Then, we declare the variables:

P = pitcher's mound
H = home plate
F = first base
S = second base
T = third base
x = the unknown variable in which we are to find its value


Step 2: Using What We Know

- so we know that the distance from the pitcher's mound to the home plate is 15.2 m.

- in reality, a pitcher's mound is usually near the centre of the baseball diamond. so we cannot use SOH CAH TOA nor can we use a^2 + b^2 = c^2

- we also know that the distance between the bases is 19.8 m which is really the side of the square.

- we now know that the baseball diamond is in fact, a square which means it will possess the properties of a square:


Flashback:

Properties of a Square:

· All sides are congruent (the same).

· All angles are congruent (the same).

· Consecutive angles of a square are supplementary. [if you find the sum of two angles of a square that are side by side (consecutive), then they will equal 180 degrees.]

· Diagonals of a square bisect each other. (if you place a diagonal line from one angle of a square to its opposite, and you do the same with the other two remaining angels, then the two diagonal lines bisect each other)

· A square has congruent diagonals. (both diagonals in a square have the same distance. for example, if a diagonal line equals 60 cm, then the other diagonal of the square would equal 60 cm)

[Note: All the information on found on Image 1 is located from the image down to this sentence.]

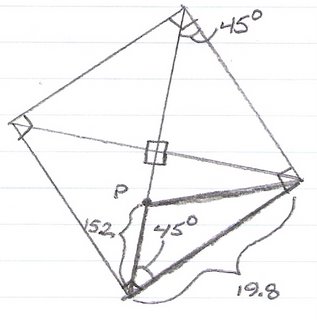
with the properties of a square in mind, all of the angles of the square equals 90 degrees and we can draw two diagonals in the baseball diamond. if that's the case, then 4 triangles, with each of its vertex on the middle of the square, magically appear on the diagram. this leads us to the fact that each angle on each corner of the square equals 45 degrees.

[Note: All the information on found on Image 2 is located from the image down to this sentence.]

Step 3: Use the Formula

believe it or not, we have all the info we need on solving this predicament. our goal is to find the distance from P to F and soon, we will have that answer. to do that, we need to look at one of the triangles and in this case, it's the FHP triangle. because we can see that FHP is not a right triangle, then we have the values of SAS (side, angle, side) we shall use the magnificent cosine law.

cosine law:

a^2 = b^2 - 2ab*cos A

in this case,

- the variable "a" refers to a side of the triange which is also known as the distance from FH. in this case, a = 19.8.

- the variable "b" refers to a side of the triange which is also known as line segment HP. in this case, b = 15.2.

- the angle refered to as "A" has the value of 45 degrees

note that variables "a" and "b" are interchangeable meaning that it does not affect the result if PH = a or PH = b OR FH = a or FH = b.

so we use the cosine forumla and bada-boom, we've got this:

a^2 = b^2 - 2ab cos A

and we plug in the numbers, bada-bing, we've got this:

(PF)^2 = 15.2^2 + 19.8^2 - 2(15.2)(19.8) cos(15.2)

and so we calulate and BAM!.....

PF= 6.497...

which having it rounded to two digits:

PF = 6.5 metres

so how far is the pitcher's mound from first base?

The pitcher's mound is 6.5 metres far from first base.

trigonoBOBetrically speaking...

People may be wondering why my BOB is on this post instead of a separate post. that's cuz i'm having technical difficulties like the font changes by itself and i couldnt log on to this website saying that my connection was reset. lol. i thought i got hacked by mz.Anonymous. lol so just bear with me

let's see...trigonometry sounds hard at first but to me it wasn't that difficult. the more i struggled with the topics given, the more knowledgeable i become. =) My "moment of clarity" was the whole "graphing-the-waves" thing. All those terms, sinusoidal axis, amplitude, DAC, sounded very confusing but mr.k explained to me step-by-step. everything on how to 'graph-the-waves' became clear to me. mr.k says that if u forget how to 'graph-the-waves', then remember DAC. Well, i remembered DAC but i dont know what it stands for...but that wont matter to me now cuz i know exactly what to do when "graphing-the-waves."