Trig Review: Trigonometrically Speaking Problem 2

LEGEND KEY

PURPLE - question/problem
GREEN - how to solve the problem
ORANGE - flashbacks
TEAL - minor notes from me (not related to trig)
GOLD - answer in sentence form


PROBLEM #2:

An 11 cm long line AB is drawn at an angle of 44 degrees to a horizontal line AE. A circle with centre B and radius 9 cm is drawn, cutting the horizontal line at points C and D. Calculate the length of the chord (line segment) CD.

First, we draw a picture:

Then, we write down and show everything we know:

- distance of AB is 11 cm

- Angle A = 44 degrees

- the radius of the circle is 9 cm meaning that BD = 9 cm and BC = 9 cm and so does the majority of AB

- if we subtract the 9 cm from the 11 cm from line segment AB, we get a leftovers of 2 cm

We know what the length of BC is, which is 9 cm, and we know BC’s opposite angle (Angle A = 44 degrees), and we also know that the length of AB is, (AB = 11 cm), yet, we do not know AB’s opposite angle, Angle C. So we say that Angle C is theta and we use the sine law.

But because we are dealing with the SIN of theta, there are two possible values because there are two known angles in Quadrant I and Quadrant II on the Cartesian Plane for sine values.

Flashback:

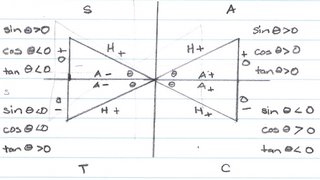
This is possible because all the SIN, COS, and TAN values of theta in Quadrant I are positive; only the SIN values of theta in Quadrant II are positive; only the TAN values of theta in Quadrant III are positive; and only the COS values of theta in Quadrant IV are positive.

This is because...

For the SIN, COS, and TAN values in Quadrant I, all values are positive because the opp osite side, the adjacent side, and the hypotenuse will always have a positive value because it is going in a positive direction. Therefore, all values of SIN, COS, and TAN, are positive when theta is at the vertex with the origin.

For the SIN, COS, and TAN values in Quadrant II,

SIN is positive because the direction of the opposite side, where theta is at the vertex with the origin, is positive because it is going in a positive direction. The hypotenuse is always positive because it is referring to distance. SIN theta = opposite/hypotenuse. Opposite is positive and hypotenuse is positive, so positive/positive = positive.

COS is negative in Quadrant II because the direction of the adjacent side , where theta is at the vertex with the origin, is negative because it is going in a negative direction. The hypotenuse is always positive because it is referring to distance. COS theta = adjacent/hypotenuse. Adjacent is negative and hypotenuse is positive, so negative/positive = negative.

TAN is negative in Quadrant II because the direction of the opposite side, where theta is at the vertex with the origin, is positive, and adjacent is negative because the adjacent side is going in a negative direction on the Cartesian Plane. TAN theta = opposite/adjacent. Opposite is positive and adjacent is negative, so positive/negative = negative.

For the SIN, COS, and TAN values in Quadrant III,

SIN is negative because the direction of the opposite side, where theta is at the vertex with the origin, is negative because it is going in a negative direction. The hypotenuse is always positive because it is referring to distance. SIN theta = opposite/hypotenuse. Opposite is negative and hypotenuse is positive, so negative/positive = negative.

COS is negative because the direction of the adjacent side, where theta is at the vertex with the origin, is negative because it is going in a negative direction. The hypotenuse is always positive because it is referring to distance. COS theta = adjacent/hypotenuse. Adjacent is negative and hypotenuse is positive, so negative/positive = negative.

TAN is positive because the direction of the opposite and the adjacent side, where theta is at the vertex with the origin, is positive because it is going in a positive direction. TAN theta = opposite/adjacent. Opposite is positive and adjacent is positive, so positive/positive = positive.

For the SIN, COS, and TAN values in Quadrant IV,

SIN is negative because the direction of the opposite side, where theta is at the vertex with the origin, is negative because it is going in a negative direction. The hypotenuse is always positive because it is referring to distance. SIN theta = opposite/hypotenuse. Opposite is negative and hypotenuse is positive, so negative/positive = negative.

COS is positive because the direction of the opposite side and the hypotenuse, where theta is at the vertex with the origin, is positive because it is going in a positive direction. The hypotenuse is always positive because it is referring to distance. COS theta =adjacent/hypotenuse. Adjacent is positive and hypotenuse is positive, so positive/positive = positive.

TAN is negative because the direction of the opposite side, where theta is at the vertex with the origin, is negative because it is going in a negative direction. The adjacent side is positive because it is going in a positive direction. TAN theta = opposite/adjacent. Opposite is negative and adjacent is positive, so negative/positive = negative.

It is easy to remember all of this stuff by remembering the mnemonic “CAST” where C is placed in Quadrant IV meaning that all and only “c”osine values are positive in that quadrant, where A is placed in Quadrant I meaning that “A”ll values are positive in that quadrant, where S is placed in Quadrant II meaning that all and only “S”ine values are positive in that quadrant, and where T is placed in Quadrant III meaning that all and only “T”angent values are positive in that quadrant.

Now back to the question...

But because we are dealing with the SIN of theta, there are two possible values because there are two known angles in Quadrant I and Quadrant II on the Cartesian Plane. So we find the related angle as shown in the diagram below.

180 degrees – 58.1 degrees = 121.9 degrees.

121.9 degrees is the related angle meaning that both 58.1 degrees AND 121.9 degrees are possible values for Angle C of Triangle BCD.

BUT...

So we have the possible values of Angle C, which is 121.9 degrees of Triangle BCD, and its opposite side, BD, which equals 9 cm. We also have the possible value of Angle D, which is 121.9 degrees so all we need is the opposite side of Angle D of T riangle BCD.

The sum of the angles of any triangle is 180 degrees. Using this triangle’s trait,

180 degrees = Angle A + Angle B + Angle C

We re-arrange the formula so we can solve for Angle B.

Angle B = 180 degrees – Angle b – Angle C

We plug-in the values...

Angle B = 180 degrees – 121.9 degrees – 121.9 degrees
Angle B = -63.8

This is not possible because there is no such thing as a negative angle in a triangle. So we refer to this as an “ambiguous case” because the problem given is not clear on a few things. Well, believe it or not, we also have evidence that was overlooked from before in this problem, meaning that this “ambiguous case” might have also been predicted. We can predict if the problem is an ambiguous case when one of the sides of a triangle can “swing” from one side to another side when a circle is involved. See below for a diagram.

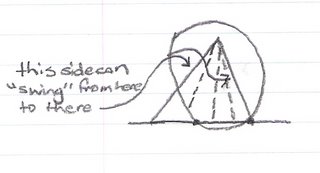
Using the process of elimination, where Angle C had two possible values: 58.1 degrees and 121.9 degrees, we now know that 121.9 degrees cannot be the answer to what we are looking for so 58.1 degrees is the answer we are looking for.

So we now know that Angle C of Triangle ABC is 121.9 degrees and Angle C of Triangle BCD is 58.1 degrees.

We know what the value of Angle C, which is 58.1 degrees, and we know the value of Angle C’s opposite side, BD, which is 9 cm, and we know that BC = 9 cm, then we can use the sine law to solve for Angle D.

Angle C & D = 180 degrees

Angle B = 180 degrees – 58 degrees – 58 degrees
Angle B = 64 degrees

We know the value of the angles C and D of triangle BCD which are both 58.1 degrees. We also know the value of the opposite side of Angle D which turns out to be 9 cm. With that in mind, we can use the sine law to finally figure out the value of CD.

The value of CD is approximately 8.59, rounded to the nearest hundredth.

yeah...so i'm still having sum technical difficulties so if the font seems all weird like this font is different than this font and u try to understand what the font pattern is, don't cuz the fonting wont change for sum "anonymous" (ha ha ha) reason. yeah...mz.anonymous will be our next scribe. in this case, it's SAMUS cuz m@rk thinks SAMUS = mz.anonymous.