Mr. K's back from his short holiday~ And so he started us off with five questions on the board. We were to solve the rest of the triangle, given one angle and the measurements of the two sides.
1. C=30°, b=10, c=5
2. C=30°, b=10, c=12
3. C=30°, b=10, c=6
4. C=30°, b=10, c=4
5. C=100°, b=10, c=8
*NOTE: It's a lot more easier if you draw out the triangle first. Just a rough sketch to let you know where things are.
To solve the other side and angles we used the pythagorean theorem.
Let's do question #1 shall we? Ok.r>
 SINB's measurement is 1. Now, punch in 2nd function, sin-1(1) in your calculator to find the angle--and you should get 90°. If you look at a wave graph you'll notice at point 1, that's where 90° is.
SINB's measurement is 1. Now, punch in 2nd function, sin-1(1) in your calculator to find the angle--and you should get 90°. If you look at a wave graph you'll notice at point 1, that's where 90° is.
Using the wave graph you can tell weather or not the triangle is possible or not. As you know, on a wave graph there is a maxiumum point and a minimum point. In this case it's -1 and 1. If your answer is somewhere lower than -1 or higher than 1 than the triangle is not possible.
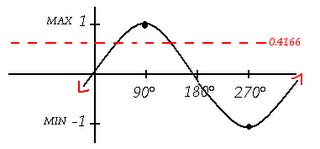
In question #2, SINB has a measurement of 0.4166. If you plot that down on a wave graph you will see that it's in between 1 and -1. It doesn't surpass the max or min points, so this makes it a possible triangle.
NOW, what is The Ambiguous Case? Well, Ambiguous means when something is not clear. For us, we were not sure which angle was the right one.
For #2 we figured out that SINB's angle is 25°. Using the unit circle graph we drew 25° on Quadrant I. But since the SIN is positive it can also be draw on Quadrant II. We aren't sure which angle would make a possible triangle.
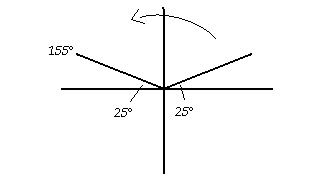
But the angle in the second quadrant is also 155°..You must have all the angles add up to 180°. since one angle is already 25°, adding 155° would make it 180° already. That's not right since a triangle has three angles.
-----------------------------------------------------------------------
Okay. I hope I explained things well enough..
NEXT SCRIBE IS.....SHAM.
The Homework for tonight is Exercise #10

Hi I was wondering did you use paint to draw the Sine Wave graph? If not, what did you use?
ReplyDeleteyes. I did use paint.
ReplyDeleteIt looks really nice that's why
ReplyDeleteHey great post, it helps me understand wave graphs now. Because i missed this unit in kelvin i will relly on this blog site( the best blog site) to help me through homework and studying. Thank you for such a good post :D
ReplyDelete-Diyaa
Great scribe MERIAN!
ReplyDeleteI really liked the way you made a connection between the graph of the sine function, the unit circle and the angles in the triangle ... a very good job explaining the ambiguous case!
The last paragraph reads ...
But the angle in the second quadrant is also 155°. You must have all the angles add up to 180°. since one angle is already 25°, adding 155° would make it 180° already. That's not right since a triangle has three angles.
That second angle you're talking about is the 30° angle given in the question. 25° and 155° have to add up to 180° because we found the 155° angle by subtracting 25° from 180°. ;-)
I think it is impressive that former students know to go to this site to find the best math notes, scribes and everything else about precal 30. Continue to write your audience is watching and reading.
ReplyDeleteMr. Harbeck
Sargent Park School